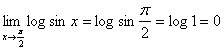§1.10
连续函数的运算与初等函数的连续性
一、连续函数的四则运算性质
由函数在一点连续的定义,不难发现,函数连续的问题仍是一个函数的极限问题,而函数极限的四则运算法则业已证明,因此,我们只要稍加改动,便可将它们移植到函数的连续。很自然地,我们有下述定理:
【定理一】有限个在某点连续的函数之和仍是一个在该点连续的函数。
【定理二】有限个在某点连续的函数的乘积仍是一个在该点连续的函数。
【定理三】两个在某点连续的函数的商仍是一个在该点连续的函数,只要分母在该点不为零。
例如:我们已知函数![]() ,
,![]() 在
在![]() 上连续,据上述定理,
上连续,据上述定理,![]() ,
, ![]() 在
在 ![]() 上也是连续的;而正切与余切函数
上也是连续的;而正切与余切函数![]() ,
,![]() 则需在分母不为零的点(即函数各自的定义域内)处才连续。
则需在分母不为零的点(即函数各自的定义域内)处才连续。
二、反函数与复合函数的连续性
【定理四】
如果函数![]() 在区间
在区间![]() 上单值,单增(或单减)且连续,则它的反函数
上单值,单增(或单减)且连续,则它的反函数![]() 也在区间
也在区间![]() 上单值,单增(或单减)且连续。
上单值,单增(或单减)且连续。
这一定理的证明从略,但对定理中的一个重要条件:
直接函数在其定义区间内必须是单值,单调,连续
要特别加以注意。
其实,这一定理可简记成:若直接函数在其定义区间上单值,单调,连续,则其反函数在其对应区间上亦然。
另外,区间![]() 实际上是直接函数的值域。
实际上是直接函数的值域。
下面, 我们来讨论反三角函数的连续性问题。
![]() 在
在![]() 上单值、单增、连续,其值域为
上单值、单增、连续,其值域为![]() 。反函数
。反函数 ![]() 在
在![]() 上亦单值、单增、连续。
上亦单值、单增、连续。
由于函数只与对应法则和定义域有关,
而与自变量的选取与关。通常,我们也用![]() 来记
来记![]() 的反函数。
的反函数。
![]() 的反函数
的反函数![]() 在
在![]() 上亦是单值、单减、连续。
上亦是单值、单减、连续。
![]() 的反函数
的反函数![]() 则在
则在![]() 上单值、单增、连续。
上单值、单增、连续。
三、复合函数的连续性定理
【定理五】
设函数![]() 当
当![]() 时的极限存在且等于
时的极限存在且等于![]() ,即
,即
![]()
而函数![]() 在点
在点![]() 连续, 则复合函数
连续, 则复合函数![]() 当
当![]() 时的极限存在且等于
时的极限存在且等于![]() , 即
, 即
![]() (1)
(1)
证明:
因![]() 在
在![]() 连续,则
连续,则 ![]() 。
。
![]() ,
,![]() ,当
,当 ![]() 时,
时,![]()
又 ![]() ,对于上述
,对于上述![]() ,
,![]() ,当
,当![]() 时,有
时,有
![]()
综合上述两个步骤有:
![]() ,
,![]() ,当
,当 ![]() 时,有
时,有
![]()
进而有:![]()
故 ![]()
![]()

2、(1)式还可写成形式 ![]() (3)
(3)
表明:求函数极限,可使用变量代换![]() 。
。
将自变量变化趋势![]() ,换成新变量变化趋势
,换成新变量变化趋势![]() ,
,
将![]() 转化为
转化为![]() (其中
(其中 ![]() )。
)。
3、定理5中的变量变化趋势![]() 可换成
可换成 ![]() , 其结论仍旧成立。
, 其结论仍旧成立。
【定理六】
设函数![]() 在
在![]() 连续,且
连续,且![]() ;而函数
;而函数![]() 在点
在点![]() 处亦连续,那么复合函数
处亦连续,那么复合函数![]() 在
在![]() 处连续。
处连续。
【证明】:只要在定理5中,令![]() 即:
即:![]() 在
在 ![]() 连续。
连续。
于是,(1)式可表示成:
![]()
这便证明了函数 ![]() 在点
在点![]() 处连续。
处连续。
【例1】求![]() (其中
(其中![]() 为正整数)
为正整数)
解:
这里:我们用到了![]() 在
在![]() 处的连续,而
处的连续,而![]() 在
在
![]() 时极限存在,且为
时极限存在,且为![]() 。
。
注:例一的解法用到了定理5的第(2)式。
【例2】求 ![]()
解:![]()
注:例二的解法用到了定理5中的第(3)式。
三、初等函数的连续性
前面,我们业已证明了三角函数和反三角函数在其定义域内是连续的。最后,我们指出(但不作详细地证明):
1、指数函数![]() 在
在![]() 内连续。
内连续。
2、对数函数![]() 在
在![]() 内连续。
内连续。
3、幂函数![]() 在其定义域(定义域要据
在其定义域(定义域要据![]() 的取值而定)内连续。
的取值而定)内连续。
总之,基本初等函数在其定义域内连续。
由基本初等函数在其定义域内的连续性,本节介绍的定理1~6可以导出如下重要而常用的结论:
一切初等函数在其定义域内都是连续的。
最后指出:如果函数![]() 在点
在点![]() 连续,那么求极限
连续,那么求极限![]() ,只需计算
,只需计算![]() 即可。这是因为,连续函数在一点的极限值应等于它在该点处的函数值。
即可。这是因为,连续函数在一点的极限值应等于它在该点处的函数值。
【例3】求![]()
![]()
解:![]() 是初等函数,在它的定义域
是初等函数,在它的定义域![]() 内是连续的,而点
内是连续的,而点![]() ,据基本结论有:
,据基本结论有: