§1.7
极限存在准则、两个重要极限
一、两边夹准则
如果数列![]() 、
、![]() 及
及![]() 满足下列条件:
满足下列条件:
(1)、![]()
(2)、![]()
那末数列![]() 的极限存在,且
的极限存在,且![]() 。
。
【证明】因
![]() ,据数列极限定义,有
,据数列极限定义,有
![]() ;
;
对于上述![]() ,
, ![]() ,
,![]() 故可取
故可取
![]()
则当
![]() 时,有
时,有 ![]() ,
,![]() 同时成立,亦即:
同时成立,亦即:
![]()
从而有 ![]()
亦即 ![]() 成立
成立
这就是说,
![]()
准则一还可推广到函数极限的情况:
如果函数![]() ,
,![]() 及
及![]() 满足下列条件:
满足下列条件:
(1)、![]() (且
(且 ![]() ),(或
),(或 ![]() )时,有
)时,有
![]()
成立;
(2)、![]()
那么,![]() 存在,且等于
存在,且等于 ![]() 。
。
二、重要极限之一 ![]()
证明: 记 ![]() , 由于
, 由于 ![]() , 我们不妨只究
, 我们不妨只究 ![]() 这一情形加以证明,如下图所示:
这一情形加以证明,如下图所示:
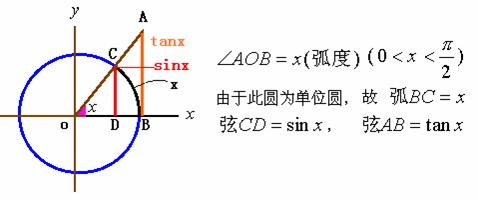
从几何图形上可清楚地看出:
![]()
于是有两边夹的不等式 ![]()
而
![]() 事实上, 当
事实上, 当 ![]() , 有:
, 有:
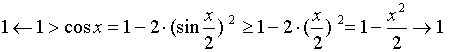
据两边夹准则,
我们有: ![]()
而
![]() 是偶函数, 故
是偶函数, 故 ![]()
由函数的左右极限的性质知,
![]()
下面, 我们给出当![]() 从1开始,以
从1开始,以 ![]() 为步长减少而趋近于
为步长减少而趋近于![]() 时,
时, ![]() 的图象的动画演示。
的图象的动画演示。

【例1】用两边夹法则证明:半径为![]() 的圆面积为
的圆面积为![]() 。
。
正多边形的面积公式为
![]() ,
,![]() 是正多边形的周长,
是正多边形的周长,![]() 是边心距。
是边心距。
如下图所示,考虑圆的内接与外接正多边形的面积![]() ,n表示正多边形的边数。
,n表示正多边形的边数。
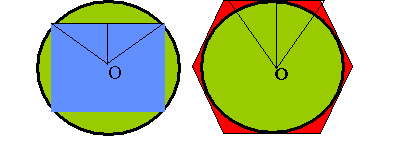
显然有:![]() ,而
,而



![]()
我们可得到圆的面积公式
![]()
![]()
至此,利用两边夹法则与1极限,用刘徽割圆术推导出了面圆积公式。借助计算机程序gs0103.m,可给出内外接正多边形夹逼圆面积的数值试验。
【例2】试证明:圆的周长与圆的直径之比为常数![]() 。
。

我们知道,![]() 时,
时,![]() (圆的周长),
(圆的周长), ![]() ,故
,故
![]()
三、单调有界准则
单调有界数列必有极限。
这一准则在几何上是非常显然的。例如:设数列![]() 单调增加且有上界A。在数轴上将数列的各项画出来, 它们严格地依次从左向右延伸,
且前方有点 A 挡住去路, 因此,这些点必在某点处产生“凝聚”,即:数列
单调增加且有上界A。在数轴上将数列的各项画出来, 它们严格地依次从左向右延伸,
且前方有点 A 挡住去路, 因此,这些点必在某点处产生“凝聚”,即:数列 ![]() 收敛。
收敛。

四、重要极限之二 ![]()
记
![]() 利用二项展开式, 我们有:
利用二项展开式, 我们有:
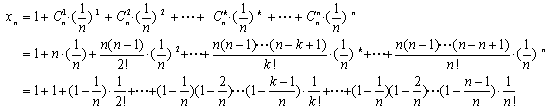

这表明数列
![]() 有界, 它位于(0,3)之间。
有界, 它位于(0,3)之间。
另一方面,
仿上面的形式, 不难写出:
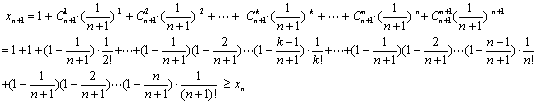
这说明,数列![]() 是单调增加的。
是单调增加的。
据准则二,
![]() 存在,记作:
存在,记作: ![]() 。
。
由![]() 的展开式有:
的展开式有:![]() ,因此, 常数
,因此, 常数![]() 。
。
由 ![]() 有
有
![]()
运行matlab程序gs0104.m,可得出![]() 时,对应的数列项
时,对应的数列项![]() 的近似值。
的近似值。
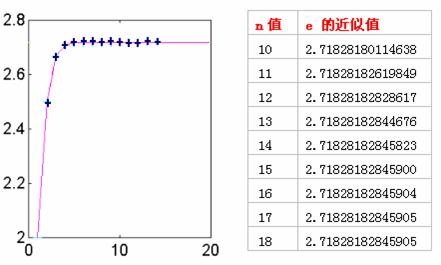
![]() 极限还可推广到更一般的情形:
极限还可推广到更一般的情形:
![]()
利用变量替换
![]() ,则
,则 ![]() ,原极限可变成一种新的形式:
,原极限可变成一种新的形式: ![]()
【例3】求 ![]()
解:
![]() , 令
, 令 ![]() , 而
, 而 ![]() ,
,
且 ![]()
原式
= 
【例4】求极限 ![]()
解:
令 ![]() ,
, ![]()


通过四个例子,可总结出如下求极限技巧。
