§1.0 序 论

一、极限思想的起源以及它的大意

极限是高等数学中一个起着基础作用的重要概念，整个高等数学的体系都建立在这一概念基础之上。

【例1】中国古代有句古语：一尺之槌，日截其半，永世不竭。

设原槌之长为一个单位长，用 表示第 n 次截取之后所剩下的长度，则。

显然，当无限地增大时， 趋近于零。所谓“永世不竭”，意指它可以无限地接近于零，但总不会等于零。对 的这一变化趋势，我们一般采用记号来表示。

这便是极限雏型，它描述地是当 时，的变化过程。

由于极限是描述变量无限渐进某个量的变化过程，使得对这一概念的理解十分困难，容易走入一些奇怪的认识误区。

二、认识误区

【例2】讨论当时，函数趋近于多少？

因为，但。因此，在求极限时，可以约去非零因子，而得到 。

而对于，很容易觉察出它的结果为2，这似乎又让了，岂不是产生了矛盾?

【例3】( 芝诺悖论 )龟兔相距一个单位长，设乌龟的爬行速度为1，而兔子的奔跑速度是乌龟速度的2倍，则兔子永远也追不上乌龟。其理由是：当兔子追到乌龟的第一个出发点时，乌龟爬行了的距离；当兔子追到乌龟的第二个起点时，乌龟又爬行了距离，…，如此下去。

这一悖论十分地迷惑人，但如果是考虑龟兔赛跑的时间，不难发现这一悖论的错误。

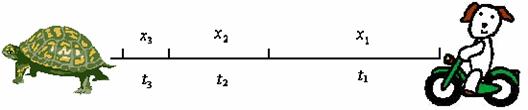
最初龟兔之间的相距

第一段路程兔子所用时间为，龟兔之间还相距

第二段路程兔子所用时间为，龟兔之间还相距

………

第n段路程兔子所用的时间为，龟兔之间还相距

前n段路程兔子所用时间的总和为

显然，当时，，这表明兔子追不上乌龟是指在单位时间内追不上，并非永远追不上。

在这一悖论中，正是由于存在着“龟兔之间的距离 无限地趋近于零，但总达不到零”这一认识上的难点，使得它容易迷惑人。

三、极限思想在数学史上所取得的成就

在初等数学中，往往只研究变量的状态性质（静态的性质），而极限是研究变量变化过程中的一种变化趋势（动态的性质）。因此，极限思想帮助我们解决了许多初等数学无法解决的问题，获得了一些令人激动不已的结果，使数学进入了一个辉煌的时期。

下面我们仅举两例，展示极限的应用方法及应用成就。

【例4】( 刘徽割圆术 )求半径为 r 的圆面积A。

正多边形的面积公式为 ， 是正多边形的周长， 是边心距。

如下图所示，考虑圆的内接与外接正多边形的面积，n表示正多边形的边数。

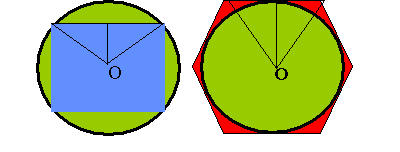
显然有： ，而

直观上，当n无限地增大时，正多边形的面积无限地趋近于圆的面积。利用著名数学软件Matlab，编写了动画程序gs0101.m，运行该程序，可更直观地了解到这一点。

由著名的极限

我们可得到圆的面积公式

【例5】( 阿基米德穷竭法 ) 求由抛物线 轴及直线 所围成的图形的面积。

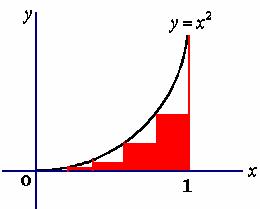
在 x 轴上从0到1的那一段区间上插入n+1个等分点

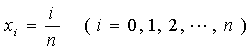
过这些点作平行于 y 轴的直线段，它们将图形划分成了n个“狭窄”的竖条，把这些“狭窄竖条”近似地看作“矩形竖条”，可求出它们面积的近似值

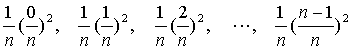
原图形面积可以用阶梯形的面积之和来近似地表示

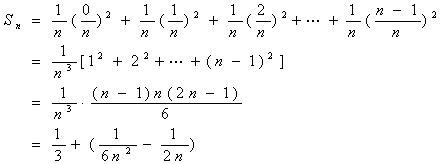
显然，当 n 愈来愈大时（即：图形分划出的竖条越来越狭窄），这个近似值就越来越接近原图形面积的真实值。也就是说，原图形面积值为