§6.3
体积
一、旋转体的体积
旋转体是由一个平面图形绕该平面内一条定直线旋转一周而生成的立体,该定直线称为旋转轴。
计算由曲线![]() 直线
直线![]() ,
,![]() 及
及![]() 轴所围成的曲边梯形,绕
轴所围成的曲边梯形,绕![]() 轴旋转一周而生成的立体的体积。
轴旋转一周而生成的立体的体积。
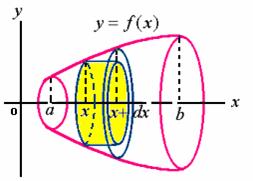
取![]() 为积分变量,则
为积分变量,则![]() ,对于区间
,对于区间![]() 上的任一区间
上的任一区间![]() ,它所对应的窄曲边梯形绕
,它所对应的窄曲边梯形绕![]() 轴旋转而生成的薄片似的立体的体积近似等于以
轴旋转而生成的薄片似的立体的体积近似等于以![]() 为底半径,
为底半径,![]() 为高的圆柱体体积。即:体积元素为
为高的圆柱体体积。即:体积元素为
![]()
所求的旋转体的体积为
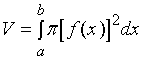
【例1】求由曲线![]() 及直线
及直线![]() ,
,![]() 和
和![]() 轴所围成的三角形绕
轴所围成的三角形绕![]() 轴旋转而生成的立体的体积。
轴旋转而生成的立体的体积。
解:取![]() 为积分变量,则
为积分变量,则![]()
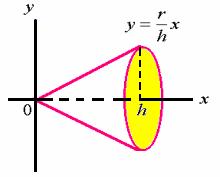

二、平行截面面积为已知的立体的体积( 截面法 )
由旋转体体积的计算过程可以发现:
如果知道该立体上垂直于一定轴的各个截面的面积,那么这个立体的体积也可以用定积分来计算。
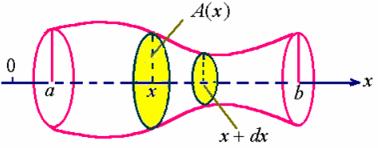
取定轴为![]() 轴, 且设该立体在过点
轴, 且设该立体在过点![]() ,
,![]() 且垂直于
且垂直于![]() 轴的两个平面之内, 以
轴的两个平面之内, 以![]() 表示过点
表示过点![]() 且垂直于
且垂直于![]() 轴的截面面积。
轴的截面面积。
取![]() 为积分变量,它的变化区间为
为积分变量,它的变化区间为![]() 。立体中相应于
。立体中相应于![]() 上任一小区间
上任一小区间![]() 的一薄片的体积近似于底面积为
的一薄片的体积近似于底面积为![]() ,高为
,高为![]() 的扁圆柱体的体积。
的扁圆柱体的体积。
即:体积元素为 ![]()
于是,该立体的体积为 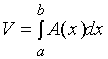
【例2】计算椭圆 所围成的图形绕
所围成的图形绕![]() 轴旋转而成的立体体积。
轴旋转而成的立体体积。
解:这个旋转体可看作是由上半个椭圆![]() 及
及![]() 轴所围成的图形绕
轴所围成的图形绕![]() 轴旋转所生成的立体。
轴旋转所生成的立体。

在![]() 处
处![]() ,用垂直于
,用垂直于![]() 轴的平面去截立体所得截面积为
轴的平面去截立体所得截面积为
![]()
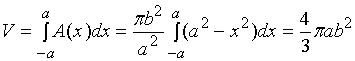
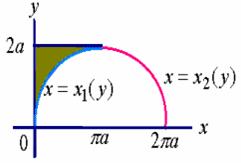
【例3】计算摆线的一拱

以及![]() 所围成的平面图形绕
所围成的平面图形绕![]() 轴旋转而生成的立体的体积。
轴旋转而生成的立体的体积。
解: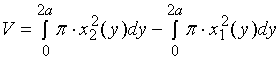
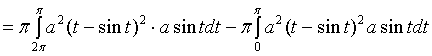

![]()
请自行计算定积分 