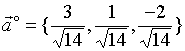§7.3
向量的坐标
一、向量在轴上的投影与投影定理
1、空间两向量的夹角
设有两向量![]() 、
、![]() 交于点
交于点![]() (若
(若![]() 、
、![]() 不相交,可将其中一个向量平移使之相交),将其中一向量绕
不相交,可将其中一个向量平移使之相交),将其中一向量绕![]() 点在两向量所决定的平面内旋转,使它的正方向与另一向量的正方向重合,这样得到的旋转角度
点在两向量所决定的平面内旋转,使它的正方向与另一向量的正方向重合,这样得到的旋转角度![]() (限定
(限定![]() )称为
)称为![]() 、
、![]() 间的夹角,记作
间的夹角,记作![]() 。
。
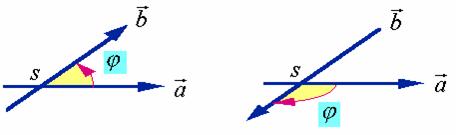
若![]() 、
、![]() 平行,当它们指向相同时,规定它们之间的夹角为
平行,当它们指向相同时,规定它们之间的夹角为![]() ;当它们的指向相反时,规定它们的夹角为
;当它们的指向相反时,规定它们的夹角为![]() 。
。
类似地,可规定向量与数轴间的夹角
将向量平行移动到与数轴相交,然后将向量绕交点在向量与数轴所决定的平面内旋转,
使向量的正方向与数轴的正方向重合, 这样得到的旋转角度![]() 称为向量与数轴的夹角。
称为向量与数轴的夹角。

2、空间点在轴上的投影
设已知点![]() 及轴
及轴![]() ,过点
,过点![]() 作轴
作轴![]() 的垂直平面
的垂直平面![]() ,则平面
,则平面![]() 与轴
与轴![]() 的交点叫做点
的交点叫做点![]() 在轴
在轴![]() 上的投影。
上的投影。
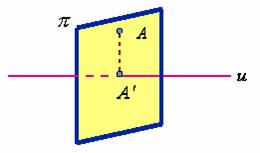
3、向量在轴上的投影
设向量![]() 的始点
的始点![]() 与终点
与终点![]() 在轴
在轴![]() 的投影分别为
的投影分别为![]() 、
、![]() , 那么轴
, 那么轴![]() 上的有向线段
上的有向线段![]() 的值
的值![]() 叫做向量
叫做向量![]() 在轴
在轴![]() 上的投影, 记作
上的投影, 记作![]() , 轴
, 轴![]() 称为投影轴。
称为投影轴。
这里,![]() 的值
的值![]() 是这样的一个数值。
是这样的一个数值。
(1)、![]() 即, 数
即, 数![]() 的绝对值等于向量
的绝对值等于向量![]() 的模。
的模。
(2)、当![]() 的方向与轴
的方向与轴![]() 的正向一致时,
的正向一致时,![]() ;当
;当![]() 的方向与
的方向与![]() 轴的正向相反时,
轴的正向相反时,![]() 。
。
4、投影定理
【定理】向量![]() 在轴
在轴![]() 上的投影等于向量的模
上的投影等于向量的模![]() 乘以轴
乘以轴![]() 与向量
与向量![]() 的夹角
的夹角![]() 的余弦。即
的余弦。即
![]()
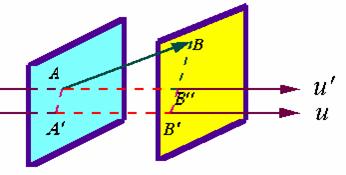
【证明】过向量![]() 的始点
的始点![]() 引轴
引轴![]() ,且轴
,且轴![]() 与轴
与轴![]() 平行且具有相同的正方向,那未轴
平行且具有相同的正方向,那未轴![]() 与向量
与向量![]() 的夹角等于轴
的夹角等于轴![]() 与向量
与向量![]() 的夹角,而且有
的夹角,而且有
![]()
![]()
故 ![]()
由上式可知:
向量![]() 在轴
在轴![]() 上的投影是一个数值,而不是向量。
上的投影是一个数值,而不是向量。
当非零向量![]() 与投影轴
与投影轴![]() 成锐角时, 向量
成锐角时, 向量![]() 的投影为正;
的投影为正;
当![]() 与投影轴
与投影轴![]() 成钝角时,向量
成钝角时,向量![]() 的投影为负;
的投影为负;
当![]() 与投影轴
与投影轴![]() 成直角时,向量
成直角时,向量![]() 的投影为零。
的投影为零。
【定理】两个向量的和在轴上的投影等于两个向量在该轴上的投影之和,即
![]()
证明:如图所示,
设![]() 为投影轴,作折线
为投影轴,作折线![]() ,
,
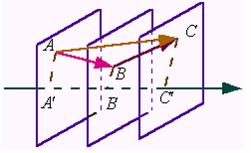
使 ![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
不论![]() 在
在![]() 轴上的位置如何,总有
轴上的位置如何,总有
![]()
![]()
即 ![]()
【推广】![]()
二、向量在坐标轴上的分向量与向量的坐标
向量的研究较复杂,为了沟通向量与数量,需要建立向量与有序数组之间的对应关系,借助向量在坐标轴上的投影可达到此目的。
1、向量在数轴上的投影向量及表示法
设![]() 是一空间向量,
是一空间向量, ![]() 为一条数轴。点
为一条数轴。点![]() 、
、![]() 在轴
在轴![]() 上的投影分别为
上的投影分别为![]() 、
、![]() ,而点
,而点![]() 、
、![]() 在数轴
在数轴![]() 上的坐标依次为
上的坐标依次为![]() 、
、![]() ,则
,则
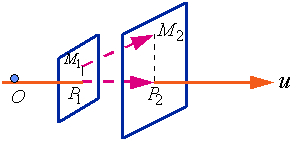
![]()
记
![]() ,则
,则 ![]() (1)
(1)
设![]() 是与轴
是与轴![]() 的正方向一致的单位向量,那么
的正方向一致的单位向量,那么
![]() (2)
(2)
(1)式是向量![]() 在轴
在轴![]() 上的投影的计算公式,而
上的投影的计算公式,而![]() 称为向量
称为向量![]() 在轴
在轴![]() 上的投影向量,(2)式是它的一种表示法。
上的投影向量,(2)式是它的一种表示法。
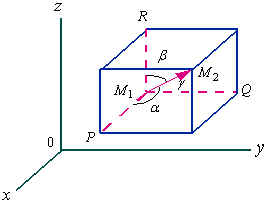
2、向量在坐标轴上的分向量
设![]() 是一空间向量,其始点为
是一空间向量,其始点为![]() ,终点为
,终点为![]() ,过点
,过点![]() 、
、![]() 各作垂直于三个坐标轴的平面,这六个平面围成一个以线段
各作垂直于三个坐标轴的平面,这六个平面围成一个以线段![]() 为对角线的长方体。
为对角线的长方体。
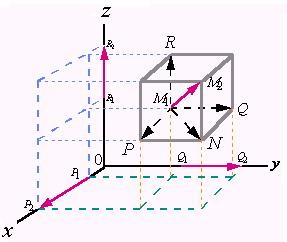
从图中可以看出
![]()
![]()
![]()
而
![]()
![]()
![]()
![]()
向量![]() 、
、![]() 、
、![]() 分别是向量
分别是向量![]() 在
在![]() 、
、![]() 、
、![]() 轴上的投影向量, 我们称它们分别是向量
轴上的投影向量, 我们称它们分别是向量![]() 在
在![]() 、
、![]() 、
、![]() 轴上的分向量。
轴上的分向量。
若以![]() 、
、![]() 、
、![]() 分别表示沿
分别表示沿![]() 、
、![]() 、
、![]() 轴正向的单位向量, 并称它们为这一坐标系的基本向量。于是
轴正向的单位向量, 并称它们为这一坐标系的基本向量。于是
![]()
![]()
![]()
因此 ![]()
或
![]()
此二式称为向量![]() 或
或![]() 按基本向量的分解式。
按基本向量的分解式。
3、向量的坐标
一方面,由向量![]() 可以唯一地定出它在三条坐标轴上的投影
可以唯一地定出它在三条坐标轴上的投影![]() ; 另一方面,由
; 另一方面,由![]() 又可以唯一地定出向量
又可以唯一地定出向量![]() 。这样,向量
。这样,向量![]() 与有序数组
与有序数组![]() 之间建立了一一对应的关系。
之间建立了一一对应的关系。
故可以把向量![]() 在三条坐标轴上的投影
在三条坐标轴上的投影![]() 叫做向量的坐标,将表达式
叫做向量的坐标,将表达式![]() 称作向量
称作向量![]() 的坐标表示式。
的坐标表示式。
注意:向量的坐标表示式是用花括号{ }表示的,不要与空间点的坐标表示式用圆括号( )表示相混淆。
以![]() 为始点及
为始点及![]() 为终点的向量的坐标式可表示成
为终点的向量的坐标式可表示成 ![]()
特别地, 空间点![]() 对于原点的向径为
对于原点的向径为
![]()
4、用坐标形式表示向量的运算性质
设
![]() ,
,![]() ,则
,则
![]() ,
,![]()
于是
![]()
![]()
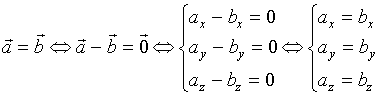
![]()
最后,我们得到了向量加减与数乘运算的坐标表示式
![]()
![]()
![]()
【例1】定比分点公式
设![]() 和
和![]() 为两已知点,有向线段
为两已知点,有向线段![]() 上的点
上的点![]() 将它分为两条有向线段
将它分为两条有向线段![]() 和
和![]() ,使它们的值的比等于数
,使它们的值的比等于数![]() (
(![]() ),即
),即
![]()
求分点![]() 的坐标。
的坐标。

解:因为![]() 与
与![]() 在同一直线上,且同方向,故
在同一直线上,且同方向,故
![]()
![]()
![]()
![]()
![]() ,
,![]() ,
,![]()
解得

三、向量的模与方向余弦的坐标表示式
向量可以用它的模与方向来表示,也可以用它的坐标式来表示,这两种表示法之间的是有联系的。
设空间向量![]() 与三条坐标轴的正向的夹角分别为
与三条坐标轴的正向的夹角分别为![]() ,规定:
,规定: ![]()
称![]() 为向量
为向量![]() 的方向角。
的方向角。
因为向量![]() 的坐标就是向量在坐标轴上的投影,因此
的坐标就是向量在坐标轴上的投影,因此
![]()
![]() (1)
(1)
![]()
公式(1)中出现的![]() 称为向量
称为向量![]() 的方向余弦。
的方向余弦。
而 ![]()
![]()
![]() 是与向量
是与向量![]() 同方向的单位向量。
同方向的单位向量。
而
![]()
![]()
![]()
![]()
![]() (2)
(2)
从而向量![]() 的方向余弦为
的方向余弦为
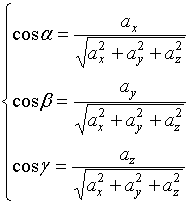 (3)
(3)
并且 ![]()
(2)、(3)式分别给出了用坐标式给出的向量![]() 的模与方向的计算公式。
的模与方向的计算公式。
【例2】已知两点![]() 和
和![]() ,求与
,求与![]() 同方向的单位向量
同方向的单位向量![]() 。
。
解:
![]()
![]()