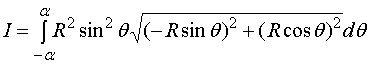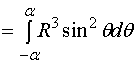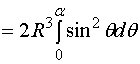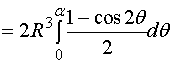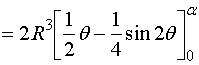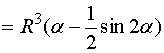§10.1 对弧长的曲线积分

一、概念的引进

假设面内有一段曲线弧具有质量,在上任一点处的线密度为,且在上连续,与分别是弧的端点,现计算弧的质量。

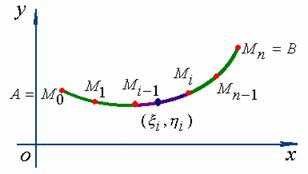
在上任意地插入个分点

将分划成个小弧段。对于第 个小弧段,由于线密度函数在上连续,当该小弧段的长度充分小时,它的质量近似地等于

于是,整个曲线弧的质量近似值为

用表示这个小弧段长度的最大者, 即

为了得到质量的精确值,只需对上述和式取极限,令,

即 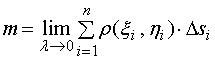(1)

撇开上例的物理意义,我们引入对弧长的曲线积分的概念。

【定义】设为面内的一条光滑曲线弧,函数在上有界,在内任意地插入点,

它把分成个小弧段,设第个小段的长度为,为上任取的一点,记

作和式

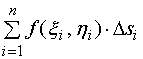
如果极限 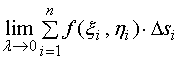存在,

这个极限值就叫做函数在曲线弧上对弧长的曲线积分,记作。

亦即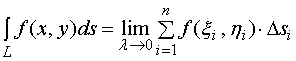

其中:叫做被积函数, 叫做积分弧段。

注记:

1、中的被积函数的定义域为上的一切点。

2、上述定义可类似地推广到空间曲线的情形,

设是空间的一条光滑曲线,函数在上有界,则

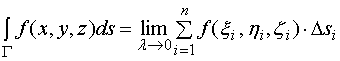
3、若为一条封闭曲线,一般将记为 。

二、对弧长的曲线积分的性质

利用对弧长的曲线积分定义, 我们可以证明下述性质

1、

2、若为常数,

3、

4、若在上,,则

5、若,则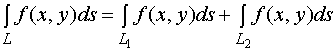

上述性质均不加以证明, 有兴趣的同学可以查阅有关书籍。

三、对弧长曲线积分的计算法

假设曲线由参数方程

给出,且函数在上具有一阶连续导数；函数在上连续；当参数由变至时, 依点至点的方向描出曲线。

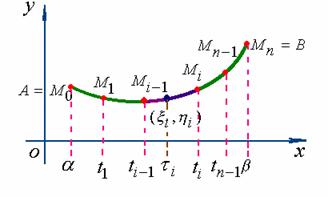
在上取一系列的点

设它们对应于一列单调增加的参数值

依定义

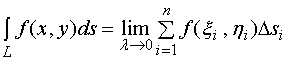
这里的,并设点对应于参数值

则

由弧长计算公式与定积分中值定理有

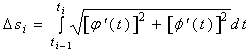
从而

(2)

由于函数在上连续, 在时,小区间的长度。 那么在上,

与

只相差一个的高阶无穷小, 因此, 我们可以把(2)式右端的换成,有

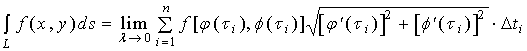
而右端和式的极限,就是函数在区间上的定积分。由于函数是连续的,故此定积分存在,因此,上式左端的曲线积分亦存在,且有

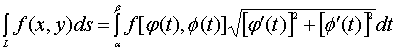(3)

强调指出, (3)式中的定积分下限一定要小于上限,理由是

(2)式中的由表达式

给出,因小弧段的长度, 从而

因此

利用(3)式,可导出如下几种对弧长的曲线积分计算公式

1、曲线由方程

给出时,

2、曲线由方程

给出时,

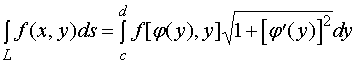
3、空间曲线由参数方程

给出时,

【例1】计算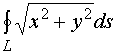,其中为圆周

【解法一】可化为参数方程

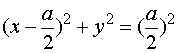
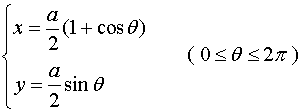
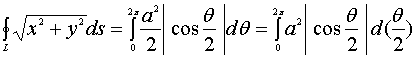
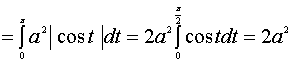
【解法二】曲线关于轴对称,设是在轴上方的一支,则方程应为

而被积函数在上关于轴偶对称,故

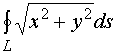
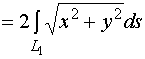
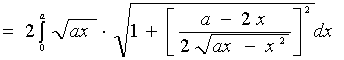
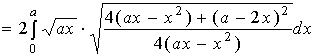
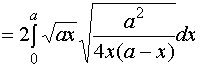
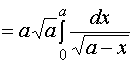
【例2】计算半径为,中心角为的圆弧对于它的对称轴的转动惯量(设线密度为)。

解:建立如图所示的坐标系

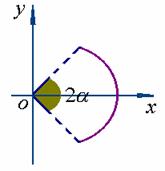
则

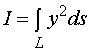
而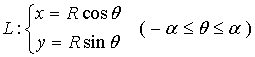

于是