§10.2 对坐标的曲线积分

一、概念的引入

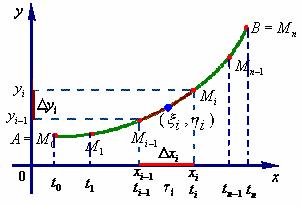
设一质点在面内从点沿光滑曲线弧移动到点,在移动过程中,该质点受到变力

的作用,其中函数,在上连续,现计算变力所作的功。

在上任意地插入个点

将划分成个小弧段,且点的坐标为 。

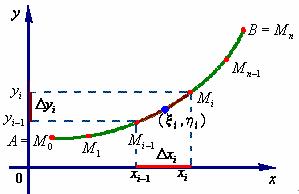
由于光滑且很短,可用有向线段

来近似地代替它,其中,,分别是在坐标轴上的投影。

又因为函数 , 在上连续,可用上任意一点处的力

来近似地代替该小弧段上的变力。

质点沿有向小弧段移动时,变力所作功可近似地取为

从而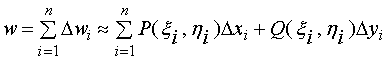

为得到的精确值,只需令,(是这个小弧段长度的最大者),对上述和式取极限。

即 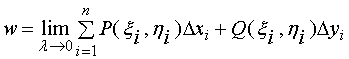(1)

(1)式右端和式的极限是又一类新的和式极限, 为此, 我们引入对坐标的曲线积分概念。

【定义】设为面内从点到点的一条有向光滑曲线弧, 函数,在上有界,用上的个点

将分成个有向小弧段,设

,

是这个小弧段长度的最大者

任取点

如果极限 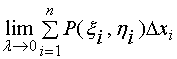存在, 则此极限值就叫做函数在有向曲线弧上对坐标的曲线积分，记作 。

类似地,如果极限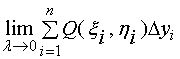存在,则此极限值就叫做函数在有向曲线弧上对坐标的曲线积分,并记作。

即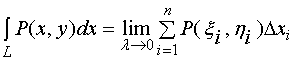

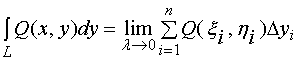
其中:,叫做被积函数,叫做积分弧段。

注记:

1、对坐标的曲线积分中的是有向弧段在轴上的投影, 它的值可正也可负。这与对弧长的曲线积分中的恒为正值是有区别的。

2、应用中经常出现

这种形式,今后,可将之简记成

从而,变力沿有向曲线所作功可表成

3、上述定义可推广到积分曲线弧为空间有向曲线弧的情形

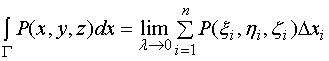
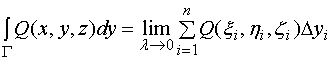
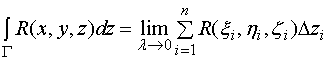
并且 可简记成形式

4、对坐标的曲线积分存在定理

若,在有向光滑曲线弧上连续,则

,

都存在。

这一定理可类似地推广到空间曲线的情形。

二、对坐标曲线积分的性质

1、若将分成与, 且,的方向由的方向所决定的,则

2、设是有向曲线弧,而是与方向相反的有向曲线弧,则

这一性质表明:对坐标的曲线积分应特别注意积分曲线弧的方向。

3、若,是常数,则

三、对坐标曲线积分计算法

【定理】

设 , 在有向曲线弧上有定义且连续；

曲线的参数方程为

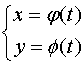
当参数单调地由变到时,点从的起点沿运动到终点；

函数,在以,为端点的区间上具有一阶连续导数,且

则曲线积分 存在,并且

(4)

证明:在上任意地插入一系列点( 依从至的方向 )

它们对应于参数值为

这一列参数值是单调变化的。

据对坐标的曲线积分定义有

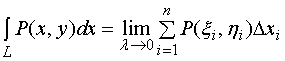
若设点对应于参数值,那么应在与之间,且

又

这里 , 而在与之间。

于是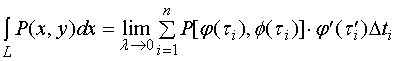

因为函数在闭区间 ( 或 )上连续, 那么可将上式中的换成,从而

而等价于,因此

上式右端的和式极限就是定积分 。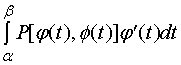

由于连续,这个定积分存在,因此上式左端的曲线积分 也就存在,且有

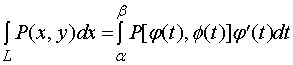
同理可证

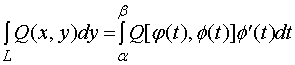
将两式相加便得到了(4)式。

几种特殊情形的对坐标曲线积分

1、如果由方程给出时,(4)式成为

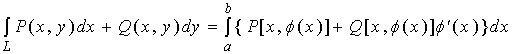
这里: 下限对应于的起点, 上限对应于的终点。

2、如果由方程给出时,(4)式成为

这里: 下限对应于的起点, 上限对应于的终点。

3、公式(4)可方便地推广到空间曲线由参数方程

给出的情形

这里:下限对应于的起点, 上限对应于的终点。

【例1】计算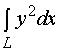, 其中为

(1)、半径为, 圆心在原点依逆时针绕行的上半圆周；

(2)、从点沿轴到点的直线段。

解1:的参数方程为

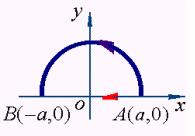
时,对应于的起点,

时,对应于的终点,

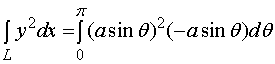
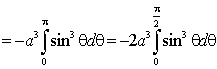
解2:的方程为,

时,对应于的起点；

时,对应于的终点,

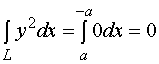
此例表明: 两个对坐标的曲线积分尽管被积函数相同, 积分曲线的起点与终点也相同,而积分曲线不同时,其值并不相同。

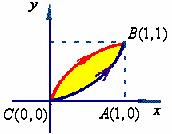
【例2】计算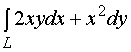, 其中为

(1)、抛物线上从到的一段弧；

(2)、抛物线上从到的一段弧；

(3)、有向折线,这里依次是, , 。

解1、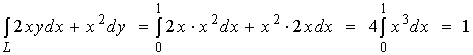

解2: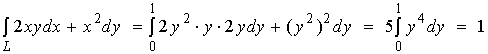

解3: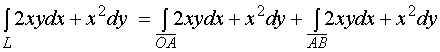

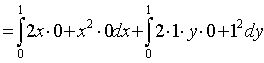
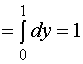
此例表明: 虽然沿不同的曲线弧,但第二类曲线积分的值可以是相同的。换句话说,计算曲线积分时, 积分值仅与起点, 终点的坐标有关, 而与连接这两点的曲线形式无关。

四、两类曲线积分的关系

设有向曲线弧的起点为,终点为,取弧长为曲线弧的参数,曲线的全长,这里。

设曲线弧由参数方程

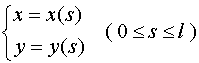
给出,函数 , 在 上具有一阶连续的导数,又函数,在上连续。

对坐标的曲线积分

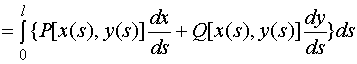
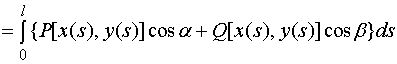
其中: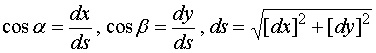

由莱布尼兹微分三角形可知: 与是有向曲线弧在点的切线向量的方向余弦,该切线向量的指向与曲线的方向一致。

另一方面,对弧长的曲线积分

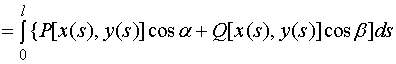
由此可见, 平面曲线上的两类曲线积分之间有如下联系

这里: 为有向曲线弧上点处的切线向量的方向角。