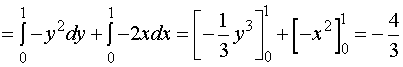§10.3
格林公式及其应用
一、格林公式
一元微积分学中最基本的公式 — 牛顿、莱布尼兹公式
表明:函数![]() 在区间
在区间![]() 上的定积分可通过原函数
上的定积分可通过原函数![]() 在这个区间的两个端点处的值来表示。
在这个区间的两个端点处的值来表示。
无独有偶,在平面区域![]() 上的二重积分也可以通过沿区域
上的二重积分也可以通过沿区域![]() 的边界曲线
的边界曲线![]() 上的曲线积分来表示,这便是我们要介绍的格林公式。
上的曲线积分来表示,这便是我们要介绍的格林公式。
1、单连通区域的概念
设![]() 为平面区域,如果
为平面区域,如果![]() 内任一闭曲线所围的部分区域都属于
内任一闭曲线所围的部分区域都属于![]() ,则称
,则称![]() 为平面单连通区域;否则称为复连通区域。
为平面单连通区域;否则称为复连通区域。
通俗地讲,单连通区域是不含“洞”(包括“点洞”)与“裂缝”的区域。
2、区域的边界曲线的正向规定
设![]() 是平面区域
是平面区域![]() 的边界曲线,规定
的边界曲线,规定![]() 的正向为:当观察者沿
的正向为:当观察者沿![]() 的这个方向行走时,
的这个方向行走时,![]() 内位于他附近的那一部分总在他的左边。
内位于他附近的那一部分总在他的左边。

简言之:区域的边界曲线之正向应适合条件,人沿曲线走,区域在左手。
3、格林公式
【定理】设闭区域![]() 由分段光滑的曲线
由分段光滑的曲线![]() 围成,函数
围成,函数![]() 及
及![]() 在
在![]() 上具有一阶连续偏导数,则有
上具有一阶连续偏导数,则有
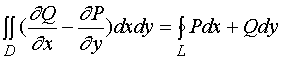 (1)
(1)
其中![]() 是
是![]() 的取正向的边界曲线。
的取正向的边界曲线。
公式(1)叫做格林(green)公式。
【证明】先证
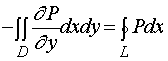
假定区域![]() 的形状如下(用平行于
的形状如下(用平行于![]() 轴的直线穿过区域,与区域边界曲线的交点至多两点)
轴的直线穿过区域,与区域边界曲线的交点至多两点)
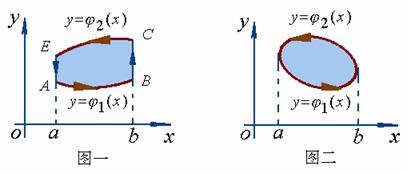
易见,图二所表示的区域是图一所表示的区域的一种特殊情况,我们仅对图一所表示的区域![]() 给予证明即可。
给予证明即可。
![]()
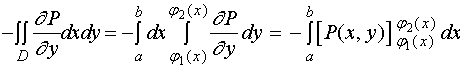
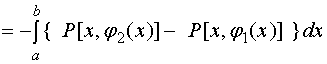
另一方面,据对坐标的曲线积分性质与计算法有
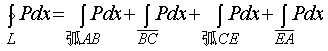

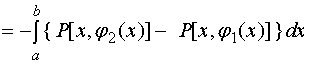
因此 
再假定穿过区域![]() 内部且平行于
内部且平行于![]() 轴的直线与的
轴的直线与的![]() 的边界曲线的交点至多是两点,用类似的方法可证
的边界曲线的交点至多是两点,用类似的方法可证
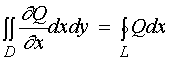
综合有
当区域![]() 的边界曲线与穿过
的边界曲线与穿过![]() 内部且平行于坐标轴(
内部且平行于坐标轴( ![]() 轴或
轴或![]() 轴 )的任何直线的交点至多是两点时,我们有
轴 )的任何直线的交点至多是两点时,我们有
 ,
, 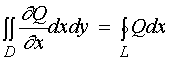
同时成立。
将两式合并之后即得格林公式
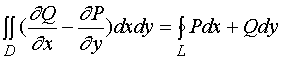
注:若区域不满足以上条件,即穿过区域内部且平行于坐标轴的直线与边界曲线的交点超过两点时,可在区域内引进一条或几条辅助曲线把它分划成几个部分区域,使得每个部分区域适合上述条件,仍可证明格林公式成立。
格林公式沟通了二重积分与对坐标的曲线积分之间的联系,因此其应用十分地广泛。
若取![]() ,
,![]() ,
, 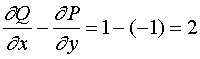 ,则格林公式为
,则格林公式为
![]()
故区域![]() 的面积为
的面积为 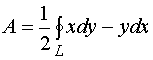
【例1】求星形线
 所围成的图形面积
所围成的图形面积![]() 。
。
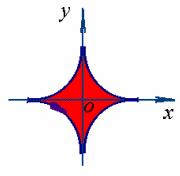
解:当![]() 从
从![]() 变到
变到![]() 时,点
时,点![]() 依逆时针方向描出了整个封闭曲线
依逆时针方向描出了整个封闭曲线![]() ,故
,故
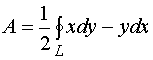

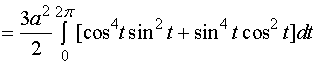
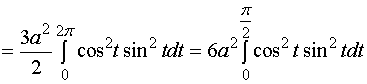
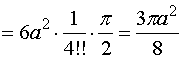
【例2】设是任意一条分段光滑的闭曲线,证明
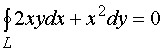
证明:这里 ![]() ,
,
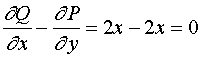
从而 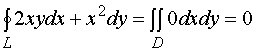
这里![]() 是由
是由![]() 所围成的区域。
所围成的区域。
二、平面曲线积分与路径无关的条件
1、对坐标的曲线积分与路径无关的定义
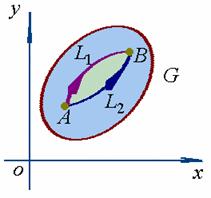
【定义一】设![]() 是一个开区域, 函数
是一个开区域, 函数![]() 、
、![]() 在
在![]() 内具有一阶连续偏导数,如果对于
内具有一阶连续偏导数,如果对于![]() 内任意两点
内任意两点![]() 、
、![]() 以及
以及![]() 内从
内从![]() 点到
点到![]() 点的任意两条曲线
点的任意两条曲线![]() 、
、![]() ,等式
,等式

恒成立,就称曲线积分![]() 在
在![]() 内与路径无关;否则,称与路径有关。
内与路径无关;否则,称与路径有关。
定义一还可换成下列等价的说法
若曲线积分与路径无关, 那么
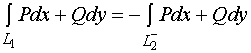
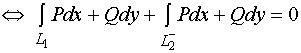


即: 在区域![]() 内由
内由![]() 所构成的闭合曲线上曲线积分为零。反过来,如果在区域
所构成的闭合曲线上曲线积分为零。反过来,如果在区域![]() 内沿任意闭曲线的曲线积分为零,也可方便地导出在
内沿任意闭曲线的曲线积分为零,也可方便地导出在![]() 内的曲线积分与路径无关。
内的曲线积分与路径无关。
【定义二】曲线积分![]() 在
在![]() 内与路径无关是指,对于
内与路径无关是指,对于![]() 内任意一条闭曲线
内任意一条闭曲线![]() ,恒有
,恒有
![]() 。
。
2、曲线积分与路径无关的条件
【定理】设开区域![]() 是一个单连通域, 函数
是一个单连通域, 函数![]() 、
、![]() 在
在![]() 内具有一阶连续偏导数,则在
内具有一阶连续偏导数,则在![]() 内曲线积分
内曲线积分![]() 与路径无关的充分必要条件是等式
与路径无关的充分必要条件是等式
![]()
在![]() 内恒成立。
内恒成立。
证明:先证充分性
在![]() 内任取一条闭曲线
内任取一条闭曲线![]() ,因
,因![]() 单连通,故闭曲线
单连通,故闭曲线![]() 所围成的区域
所围成的区域![]() 全部在
全部在![]() 内。从而
内。从而 ![]() 在
在![]() 上恒成立。
上恒成立。
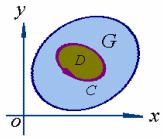
由格林公式,有
![]()
![]()
依定义二,在![]() 内曲线积分
内曲线积分![]() 与路径无关。
与路径无关。
再证必要性(采用反证法)
假设在![]() 内等式
内等式![]() 不恒成立,那么
不恒成立,那么![]() 内至少存在一点
内至少存在一点![]() ,使
,使
![]()
不妨设
![]()
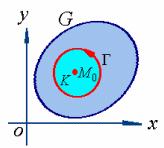
由于![]() 在
在![]() 内连续,在
内连续,在![]() 内存在一个以
内存在一个以![]() 为圆心,半径充分小的圆域
为圆心,半径充分小的圆域![]() ,使得在
,使得在![]() 上恒有
上恒有
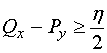
由格林公式及二重积分性质有
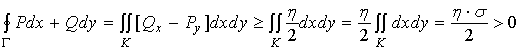
这里![]() 是
是![]() 的正向边界曲线,
的正向边界曲线,![]() 是
是![]() 的面积。
的面积。
这与![]() 内任意闭曲线上的曲线积分为零的条件相矛盾。故在
内任意闭曲线上的曲线积分为零的条件相矛盾。故在![]() 内等式
内等式
![]()
应恒成立。
注明:定理所需要的两个条件

缺一不可。
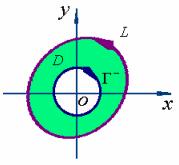
【反例】讨论 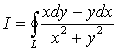 ,其中
,其中![]() 是包围原点的一条分段光滑曲线且正向是逆时针的。
是包围原点的一条分段光滑曲线且正向是逆时针的。
这里 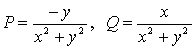
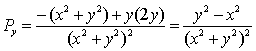 ,
, 
除去原点外,![]() 在
在![]() 所围成的区域内存在、连续,且
所围成的区域内存在、连续,且 ![]() 。
。
在![]() 内,作一半径充分小的圆周
内,作一半径充分小的圆周 ![]()
在由![]() 与
与![]() 所围成的复连通域内使用格林公式有
所围成的复连通域内使用格林公式有
![]()
![]()
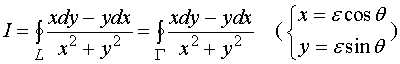
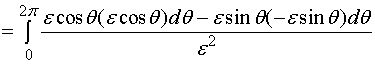
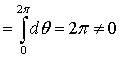
三、二元函数的全微分求积
若曲线积分![]() 在开区域
在开区域![]() 内与路径无关,那它仅与曲线的起点与终点的坐标有关。假设曲线
内与路径无关,那它仅与曲线的起点与终点的坐标有关。假设曲线![]() 的起点为
的起点为![]() ,终点为
,终点为![]() ,可用记号
,可用记号
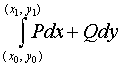 或
或 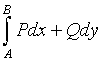
来表示,而不需要明确地写出积分路径。
显然,这一积分形式与定积分非常相似, 事实上,我们有下列重要定理
【定理一】设![]() 是一个单连通的开区域,函数
是一个单连通的开区域,函数![]() 、
、![]() 在
在![]() 内具有一阶连续偏导数,且
内具有一阶连续偏导数,且 ![]() ,则
,则

是![]() 的单值函数,这里
的单值函数,这里![]() 为
为![]() 内一固定点,且
内一固定点,且
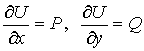
亦即 ![]()
【证明】依条件知,对![]() 内任意一条以点
内任意一条以点![]() 为起点,点
为起点,点![]() 为终点的曲线
为终点的曲线![]() ,曲线积分
,曲线积分 ![]() 与路径
与路径![]() 无关,仅与
无关,仅与![]() 的起点和终点的坐标有关,亦即,
的起点和终点的坐标有关,亦即, ![]() 确为点
确为点![]() 的单值函数。
的单值函数。
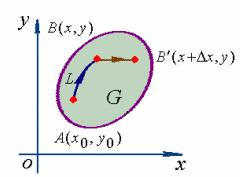
下面证明
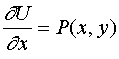
由于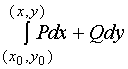 可以认为是从点
可以认为是从点![]() 沿
沿![]() 内任何路径到点
内任何路径到点![]() 的曲线积分,取如下路径,有
的曲线积分,取如下路径,有

![]()
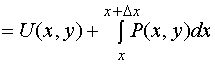
![]()
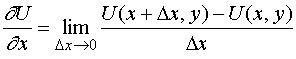
![]()
类似地可证明
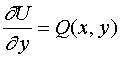
因此
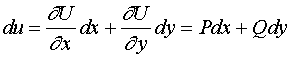
【定理二】设![]() 是单连通的开区域,
是单连通的开区域,![]() 、
、![]() 在
在![]() 上具有一阶连续偏导数,则
上具有一阶连续偏导数,则![]() 在
在![]() 内为某一函数
内为某一函数![]() 全微分的充要条件是
全微分的充要条件是
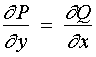
在![]() 内恒成立。
内恒成立。
【证明】显然,充分性就是定理一
下面证明必要性
若存在![]() 使得
使得 ![]() ,则
,则

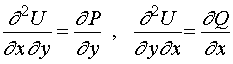
由于
![]() 、
、![]() 在
在 ![]() 内连续, 则二阶混合偏导数适合等式
内连续, 则二阶混合偏导数适合等式
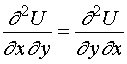
从而 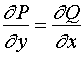
【定理三】设![]() 是一个单连通的开区域, 函数
是一个单连通的开区域, 函数![]() 、
、![]() 在
在![]() 内具有一阶连续偏导数, 若存在二元函数
内具有一阶连续偏导数, 若存在二元函数![]() 使得
使得
![]()
则
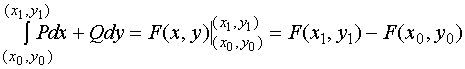
其中![]() 、
、![]() 是
是![]() 内的任意两点。
内的任意两点。
【证明】由定理1知,函数 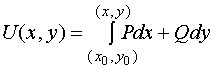
适合 ![]()
于是
![]() 或
或 ![]()
因此
![]() (
(![]() 是某一常数 )
是某一常数 )
![]()
![]()
即 ![]()
而 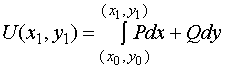

这是因为由点![]() 沿任意
沿任意![]() 内的路径回到点
内的路径回到点![]() 构成一条封闭曲线,故
构成一条封闭曲线,故 ![]()
因此
 □
□
【确定![]() 的全微分函数
的全微分函数![]() 的方法】
的方法】
因为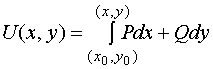 ,而右端的曲线积分与路径无关,为了计算简便,可取平行于坐标轴的直线段所连成的折线作为积分路径(当然折线应完全属于单连通区域)。
,而右端的曲线积分与路径无关,为了计算简便,可取平行于坐标轴的直线段所连成的折线作为积分路径(当然折线应完全属于单连通区域)。
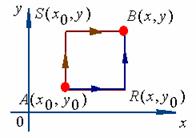

或 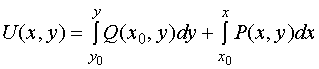
【例3】验证:在整个![]() 面内,
面内, ![]() 是某个函数的全微分,并求出一个这样的函数。
是某个函数的全微分,并求出一个这样的函数。
解:
![]()
且![]() , 在整个
, 在整个![]() 面内恒成立。因此,在整个
面内恒成立。因此,在整个![]() 面上,
面上, ![]() 是某个函数的全微分, 设此函数为
是某个函数的全微分, 设此函数为![]() ,则
,则
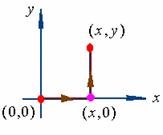
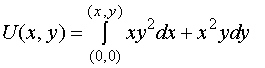
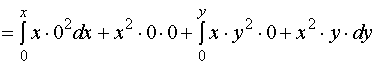
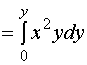
![]()
【例4】计算  。
。
解: