§10.4 对面积的曲面积分

一、概念的引入

1、引例

我们知道，若为面上具有质量密度为的一块薄片，那么该平面薄片的质量可以由如下二重积分表示

当是一张具有质量密度 的空间曲面时，它也具有质量，那么它的质量应如何定义和计算呢？显然，解决这一问题的方法仍可用我们曾反复使用过的元素法。

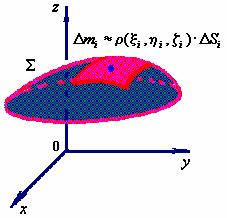
用任意一组曲线将曲面划分成块“小”曲面(既表示第块“小”曲面，也表示它的面积)，若面密度函数在上连续的条件下，第块“小”曲面的质量近似地为

其中是上的任意一点。

于是，曲面的总质量近似地为

从而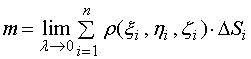

这里，表示块“ 小 ”曲面直径中最大者。

撇开这一实际问题的具体意义，抽出它所蕴含的数学特征，便有如下对面积的曲面积分的概念。

2、对面积的曲面积分的定义

设空间曲面是光滑的，函数在上有界，用任意一组曲线将划分成个小块( 同时也表示第 小块曲面的面积 )，在第小块上任意取定一点，作和式

用记各小块曲面直径中的最大者， 如果当时，上述和式的极限存在，则称此极限值为函数在曲面上对面积的曲面积分，并记作

，亦即

其中：叫做被积函数，叫做积分曲面，叫做曲面面积元素。

根据上述定义，面密度为连续函数的光滑曲面的质量，可以表示成为函数在上对面积的曲面积分

对面积的曲面积分在物理上表示具有质量分布曲面的总质量，这与二重积分所代表的物理意义是相同的，因此，它有与二重积分相类似的一些性质。

二、对面积的曲面积分的性质

1、存在定理

若曲面是光滑的，函数在曲面上连续，则

存在。

2、对曲面的可加性

设可分成两片光滑的曲面与( 记作 )，而

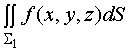与

均存在，则亦存在，且有

3、

4、若在曲面上，有 ，则

三、对面积的曲面积分的计算法

设曲面由方程给出，它在面上的投影区域为，函数在上具有一阶连续偏导数，而被积函数在上连续。

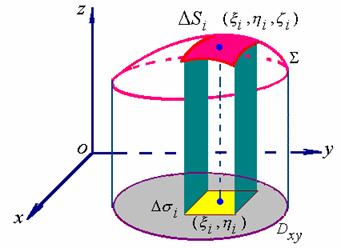
依对面积的曲面积分定义有

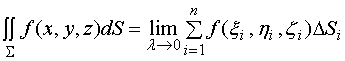
如图，第块小曲面( 它的面积也记作) 在面上投影区域为( 它的面积也记作 )，则可表示成

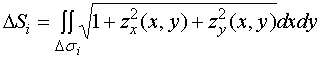
点属于曲面，故

于是，积分和式可表示成

由于函数以及函数在闭区域上连续，当时，上式右端的极限与

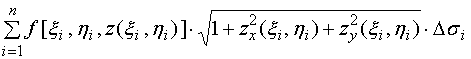
的极限是相等的，都等于二重积分

因此

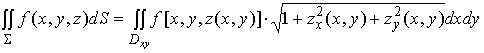
这就是对面积的曲面积分化二重积分的计算公式。

注一、公式的记忆方法

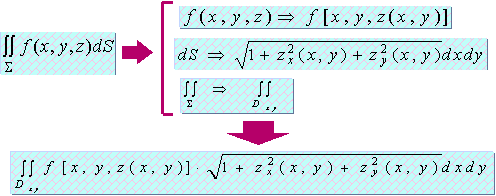
注二、被积函数定义在上，它的自变量取值应满足方程。

注三、用类似的方法，可导出对面积的曲面积分另外两个计算公式。

【例1】求，为锥面介在之间的部分。

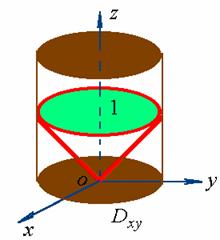
【解法一】取的方程为

它在面上的投影区域为

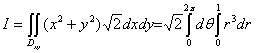
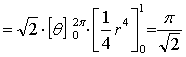
【解法二】取的方程为

那么在面上的投影区域为

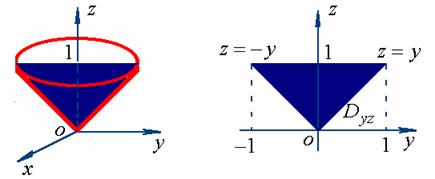
曲面关于面分前后对称的两片，只考虑前面的一片，然后使用对称性即可。

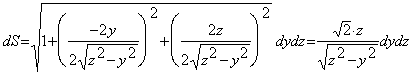
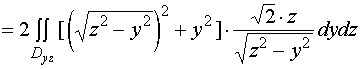
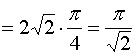
由此例的两种解法，可总结出对面积的曲面积分计算的两大要点：

1、给出曲面合适的方程形式

( 或 )

2、找出曲面在相应的坐标面 (或 ) 上的投影区域

( 或 )。

如果曲面方程的选择不适宜，会给投影区域的确定与二重积分的计算造成一定的困难。

【例2】求均匀曲面的重心坐标。

解：设面密度为，重心坐标为 ，依重心的定义有

其中，是曲面的总质量，， ， 为曲面对坐标面，， 的力矩。

曲面在面的投影区域为 ，

曲面的面积元素为

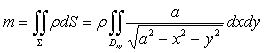
故 ，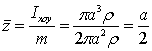

由曲面的对称性，有

，

从而 ，重心坐标为。