§10.5 对坐标的曲面积分
一、曲面的侧、曲面在坐标面上的投影区域
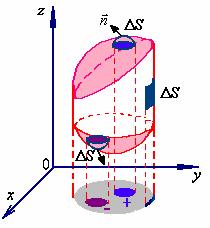
假定我们所讨论的曲面是光滑的,一般来讲,我们所遇到的曲面都是双侧的,曲面侧可以通过曲面上法向量的指向来定义,这种取定了法向量也就选定了侧的曲面,我们称之为有向曲面。


![]() 是有向曲面,在
是有向曲面,在![]() 上取一小块曲面
上取一小块曲面![]() ,设
,设![]() 是
是![]() 的法向量与
的法向量与![]() 轴正向的夹角
轴正向的夹角![]() 的余弦,
的余弦,![]() 是
是![]() 在
在![]() 面投影区域的面积值。我们规定:
面投影区域的面积值。我们规定:![]() 在
在![]() 面上的投影
面上的投影![]() 为
为
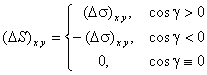
其中![]() 也就是
也就是![]() 的情形。
的情形。
简言之:![]() 在
在![]() 面上的投影
面上的投影![]() ,实际就是
,实际就是![]() 在
在![]() 面上的投影区域的面积附以一定的正负号,即:
面上的投影区域的面积附以一定的正负号,即:![]() 。
。
类似地可以定义![]() 在
在![]() 面及
面及![]() 面上的投影
面上的投影![]() 及
及![]() 。
。
二、流向曲面一侧的流量
设稳定流动的不可压缩流体(假定密度为1)的速度场由
![]()
给出,![]() 是速度场中的一片有向曲面,函数
是速度场中的一片有向曲面,函数![]() 均在
均在![]() 上连续,求单位时间内流向
上连续,求单位时间内流向![]() 指定侧的流体的质量,即流量
指定侧的流体的质量,即流量![]() 。
。
先讨论一个特殊情况:如果流体流过平面上面积为![]() 的一个闭区域,且流体在该闭区域上各点的流速为(常向量)
的一个闭区域,且流体在该闭区域上各点的流速为(常向量)![]() ,设
,设![]() 为该平面的单位法向量。
为该平面的单位法向量。
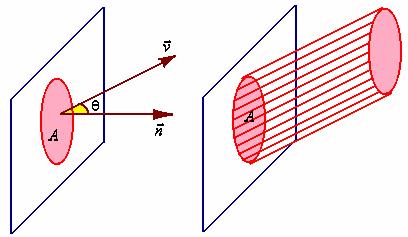
显然,在单位时间内流过该闭区域的流体组成一个底面积为![]() ,斜高为
,斜高为![]() 的斜柱体。
的斜柱体。
1、当![]() 时,这斜柱体的体积为
时,这斜柱体的体积为 ![]() ,这就是通过闭区域
,这就是通过闭区域![]() 流向
流向![]() 所指一侧的流量;
所指一侧的流量;
2、当![]() 时,显然流体通过闭区域
时,显然流体通过闭区域![]() 流向
流向![]() 所指一侧的流量为零,而
所指一侧的流量为零,而![]() ;
;
3、当![]() 时
时![]() ,它表示流体通过闭区域
,它表示流体通过闭区域![]() 实际上流向
实际上流向![]() 所指一侧,且流向
所指一侧,且流向![]() 所指一侧的流量为
所指一侧的流量为![]() 。因此,不论
。因此,不论![]() 为何值,流体通过闭区域
为何值,流体通过闭区域![]() 流向
流向![]() 所指向一侧的流量均为
所指向一侧的流量均为![]() 。
。
再讨论一般情况:流体流过的是一片曲面,且流速![]() 是变化的,此时的流量计算不能直接用上述方法,必须使用元素法来处理。
是变化的,此时的流量计算不能直接用上述方法,必须使用元素法来处理。
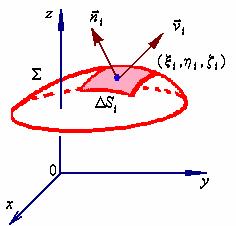
把曲面![]() 分成
分成![]() 小块
小块![]() (
(![]() 同时也代表第
同时也代表第![]() 小块曲面的面积)。在
小块曲面的面积)。在![]() 是光滑的和
是光滑的和![]() 是连续的前提下,只要
是连续的前提下,只要![]() 的直径很小,我们就可以用
的直径很小,我们就可以用![]() 上任一点
上任一点![]() 处的流速
处的流速
![]()
代替![]() 上其它各点处的流速,以该点
上其它各点处的流速,以该点![]()
![]()
处曲面![]() 的单位法向量
的单位法向量
![]()
代替![]() 上其它各点处的单位法向量,从而得到通过
上其它各点处的单位法向量,从而得到通过![]() 流向指定侧的流量的近似值为
流向指定侧的流量的近似值为
![]()
于是,通过![]() 流向指定侧的流量
流向指定侧的流量
![]()
![]()
但 ![]() ,
,![]() ,
,![]()
因此上式又可写成
![]()
令![]() 取上述和式的极限,就得到流量
取上述和式的极限,就得到流量![]() 的精确值。
的精确值。
这样的极限还会在其它问题中遇到,抽去它们的具体意义,可给出对坐标的曲面积分概念。
三、对坐标的曲面积分定义及性质
【定义】设![]() 为光滑的有向曲面,函数
为光滑的有向曲面,函数![]() 在
在![]() 上有界。把
上有界。把![]() 任意分成
任意分成![]() 块小曲面
块小曲面![]() (
(![]() 同时又表示第
同时又表示第![]() 块小曲面的面积),
块小曲面的面积),![]() 在
在![]() 面上的投影为
面上的投影为![]() ,
,![]() 是
是![]() 上任意取定的一点,如果当各小块曲面的直径的最大值
上任意取定的一点,如果当各小块曲面的直径的最大值![]() 时,极限
时,极限
![]()
![]()
总存在,则称此极限为函数![]() 在有向曲面
在有向曲面![]() 上对坐标
上对坐标![]() 的曲面积分,并记作
的曲面积分,并记作 ![]() 。
。
即 ![]()
其中![]() 叫做被积函数,
叫做被积函数,![]() 叫做积分曲面。
叫做积分曲面。
类似地可以定义
函数![]() 在有向曲面
在有向曲面![]() 上对坐标
上对坐标![]() 的曲面积分
的曲面积分![]() ,即
,即
![]()
函数![]() 在有向曲面
在有向曲面![]() 上对坐标
上对坐标![]() 的曲面积分
的曲面积分![]() ,即
,即
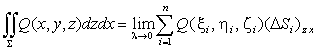
以上三个曲面积分也称为第二类曲面积分。
我们指出,当![]() ,
,![]() ,
,![]() 在有向光滑曲面
在有向光滑曲面![]() 上连续时,对坐标的曲面积分是存在的,以后总假定
上连续时,对坐标的曲面积分是存在的,以后总假定![]() 在
在![]() 上连续。
上连续。
在应用上出现较多的是形式
![]()
为简便起见,我们把它写成
![]()
例如,上述流向![]() 指定侧的流量
指定侧的流量![]() 可表示成为
可表示成为
![]()
如果![]() 是分片光滑的有向曲面,我们规定函数在
是分片光滑的有向曲面,我们规定函数在![]() 上对坐标的曲面积分等于函数在各片光滑曲面上对坐标的曲面积分之和。
上对坐标的曲面积分等于函数在各片光滑曲面上对坐标的曲面积分之和。
对坐标的曲面积分与对坐标的曲线积分有着相类似的一些性质。
1、如果把![]() 分成
分成![]() 和
和![]() ,则
,则
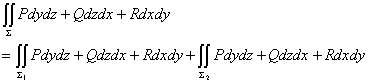 (1)
(1)
公式(1)可以推广到![]() 被分成了
被分成了![]() 几部分的情形。
几部分的情形。
2、设![]() 是有向曲面,
是有向曲面,![]() 表示与
表示与![]() 取相反侧的有向曲面,则
取相反侧的有向曲面,则
![]()
![]() (2)
(2)
![]()
(2)式表明:当积分曲面改变为相反侧时,对坐标的曲面积分要改变符号,因此关于对坐标的曲面积分我们必须注意积分曲面所取的侧。
这些性质的证明从略。
四、对坐标的曲面积分的计算法![]()
设积分曲面![]() 是由方程
是由方程![]() 所给出的曲面的上侧,
所给出的曲面的上侧,![]() 在
在![]() 面上的投影区域为
面上的投影区域为![]() ,假设函数
,假设函数![]() 在
在![]() 上具有一阶连续偏导数,
上具有一阶连续偏导数,![]() 在
在![]() 上连续。
上连续。
按对坐标的曲面积分的定义,有
![]()
因为![]() 取上侧,
取上侧,![]() ,所以
,所以
![]()
又因![]() 是
是![]() 上的一点,故
上的一点,故![]() ,从而有
,从而有
![]()
令![]() 取上式两端的极限,就得到
取上式两端的极限,就得到
![]() (3)
(3)
这就将对坐标的曲面积分化为了二重积分。
公式(3)表明:计算对坐标的曲面积分![]() 时,只要把其中变量
时,只要把其中变量![]() 换成
换成![]() 方程
方程![]() ,然后在
,然后在![]() 的投影区域
的投影区域![]() 上计算二重积分就成了。
上计算二重积分就成了。
必须注意:公式(3)的曲面积分是取在曲面![]() 上侧的;如果曲面积分取在曲面
上侧的;如果曲面积分取在曲面![]() 下侧,这时
下侧,这时![]() ,那末
,那末
![]()
从而有
![]() (3’)
(3’)
类似地,如果![]() 由
由![]() 给出,则有
给出,则有
![]() (4)
(4)
等式右端的符号这样决定:若积分曲面![]() 是由方程
是由方程![]() 所给出的曲面前侧,即
所给出的曲面前侧,即![]() ,应取正号;反之,如果
,应取正号;反之,如果![]() 取后侧,即
取后侧,即![]() ,应取负号。
,应取负号。
如果![]() 由
由![]() 给出,则有
给出,则有
![]() (5)
(5)
等式右端的符号这样决定:若积分曲面![]() 是方程
是方程![]() 所给出的曲面右侧,即
所给出的曲面右侧,即![]() ,应取正号;反之,如果
,应取正号;反之,如果![]() 取左侧,即
取左侧,即![]() ,应取负号。
,应取负号。
【例1】计算曲面积分
![]()
其中![]() 是球面
是球面![]() 外侧在
外侧在![]() 的部分。
的部分。
解:把![]() 分为
分为![]() 和
和![]() 两部分,则
两部分,则
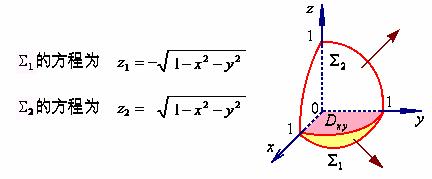
![]()
上式右端的第一个积分的积分曲面![]() 取下侧,第二个积分的积分曲面
取下侧,第二个积分的积分曲面![]() 取上侧,因此分别应用公式(3’)及(3),就有
取上侧,因此分别应用公式(3’)及(3),就有
![]()
其中![]() ,利用极坐标计算这个二重积分如下:
,利用极坐标计算这个二重积分如下:
![]()
![]()
![]()
从而 ![]()
五、两类曲面积分之间的联系
设![]() 是由方程
是由方程![]() 给出的曲面上侧,由对坐标曲面积分计算公式有
给出的曲面上侧,由对坐标曲面积分计算公式有
![]()
另一方面,![]() 的法向量的方向余弦为
的法向量的方向余弦为
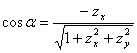 ,
, ,
,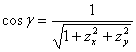
由对面积的曲面积分计算公式有
![]()
由此可见,有
![]() (6)
(6)
如果![]() 取下侧,则有
取下侧,则有
![]()
此时,![]() 的法向量的方向余弦应取为
的法向量的方向余弦应取为
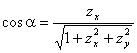 ,
,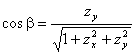 ,
,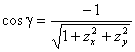
![]()
因此(6)式仍成立。
类似地,我们可导出关系式
![]() (7)
(7)
![]() (8)
(8)
合并(6),(7),(8)三式,得两类曲面积分之间的如下联系:
![]() (9)
(9)
其中![]() 是有向曲面
是有向曲面![]() 在点
在点![]() 处的法向量的方向余弦。
处的法向量的方向余弦。
若引入记号:
![]() ,
,![]() ,
,![]()
由(9)式有
![]()
两类曲面积分的关系式可简单地表示为
![]()
我们称 ![]() 为有向曲面元。
为有向曲面元。
【例2】计算曲面积分
![]()
其中![]() 是旋转抛物面
是旋转抛物面![]() 介于平面
介于平面![]() 及
及![]() 之间部分的下侧。
之间部分的下侧。
解法一:

由两类曲面积分之间的关系式,有
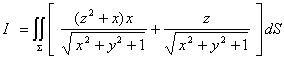
![]()
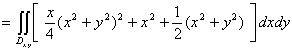
利用二重积分的性质,![]() ,于是
,于是
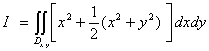
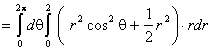
![]()
解法二:由两类曲面积分的关系式,有
![]()
在曲面![]() 上,有
上,有
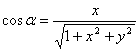 ,
,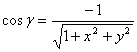
故 ![]()
![]()
![]()
再按对坐标曲面积分的计算法,有
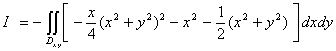
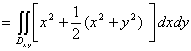
![]()