§10.6 高斯公式 通量与散度
一、高斯公式
格林公式表达了平面闭区域上的二重积分与其边界曲线上的曲线积分之间的关系,而高斯公式表达了空间闭区域上的三重积分与其边界曲面上的曲面积分之间的关系，这个关系可陈述如下：
【定理】设空间闭区域
是由分片光滑的闭曲面
所围成，函数
、
、
在上具有一阶连续偏导数，则有
(1)
或 
(
)
这里
是的整个边界曲面的外侧，
是上点
处的法向量的方向余弦,公式(１)或()叫做高斯公式。
证：由两类曲面积分的关系，公式(1)与()的右端是相等的，因此这里只要证明公式(1)就可以了。
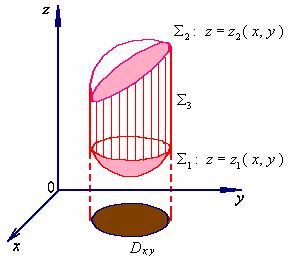
设闭区域在
面上的投影区域为
，假定穿过内部且平行
轴的直线与的边界曲面的交点恰好是两个。这样，可设由
，
和
三部分组成，其中和分别由方程
和
给定，这里
，取下侧，取上侧；是以的边界曲线为准线而母线平行于轴的柱面上的一部分，取外侧。
根据三重积分的计算法，有
(2)
因为上任意一块曲面在面上的投影为零，所以直接根据对坐标的曲面积分的定义可知
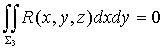
把以上三式相加，得
(3)
比较(2)、(3)两式，得
如果穿过内部且平行于
轴的直线以及平行于
轴的直线与的边界曲面的交点恰好有两点，那么类似地可得
把以上三式两端分别相加，即得高斯公式(1)。
在上述证明中，我们对闭区域作了这样的限制，即穿过内部且平行于坐标轴的直线与的边界曲面
的交点恰好是两点。如果 不满足这样的条件，可以引进几张辅助曲面把分为有限个闭区域，使得每个闭区域满足这样的条件，并注意到沿辅助曲面相反两侧的两个曲面积分的绝对值相等而符号相反，相加时正好抵消，因此公式(1)对于这样的闭区域仍然是正确的。
【例1】利用高斯公式计算曲面积分
其中为柱面
及
，
所围成的空间区域的整个边界曲线的外侧。
解：这里
，
，
，
，
，
利用高斯公式把所给曲面积化为三重积分，再利用柱面坐标计算三重积分：
【例2】利用高斯公式计算曲面积分
其中为锥面
介于平面及
之间的部分的下侧，
、
、
是在点处的法向量的方向余弦。
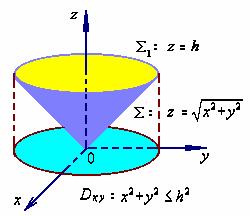
解：曲面不是封闭曲面，不能直接利用高斯公式，补充曲面
则与一起构成一个封闭曲面，记它们所围成的空间闭区域为，利用高斯公式，便有
其中
，注意到
即得
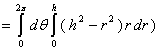
而
因此
【例3】设函数
和
在闭区域上具有一阶及二阶连续偏导数，试证明
其中是闭区间的整个边界曲面，
为函数沿的外法线方向的方向导数，这个公式叫做格林第一公式。
证：在高斯公式
中，令
，
，
，并分别代入上式的左右两边，便得到
上述两式结合便是所要证明的格林第一公式。
*二、沿任意闭曲面的曲面积分为零的条件
设
是起点为
、终点为
的光滑曲线，对于曲线积分
若被积函数满足
，上述曲线积分与无关而只与、坐标有关。
很自然地，我们会想到这样的一个问题，在怎样的条件下，曲面积分
与曲面无关而只与的边界曲线有关？这问题相当于在怎样条件下，沿任意封闭曲面的曲面积分为零？这个问题可用高斯公式来解决。
先介绍空间二维单连通及一维单连通区域的概念。
对空间区域
，如果内任一闭曲面所围成的区域全属于，则称是空间二维单连通区域；如果内任一闭曲线总可以张一片完全属于的曲面，则称为空间一维单连通区域。
对于沿任意闭曲面的曲面积分为零的条件，我们有以下结论：
【定理】设是空间二维单连通区域，函数、、在内具有一阶连续偏导数，则曲面积分
在内与所取曲面无关而只取决于的边界曲线(或沿内任一闭曲面的曲面积分为零)的充分必要条件是等式
(4)
在内恒在成立。
证：若等式(4)在内恒成立，则由高斯公式(1)立即可看出沿内的任意曲面的曲面积分为零，因此条件(４)是充分的。
反之，设内的任一闭曲面的曲面积分为零，若等式(4)在内不恒成立，就是说在内至少有一点
使得
仿照第10.3节第二目中所用的方法，就可得出内存在着闭曲面使得沿该闭曲面的曲面积分不等于零，这与假设相矛盾。因此条件(4)是必要的。
三、通量与散度
下面来解释高斯公式
(1)
的物理意义。
设稳定流动的不可压缩液体(假定密度为1)的速度场由
给出，其中
、
、
假定具有一阶连续偏导数，是速度场中一片有向曲面，又
是在点处的单位法向量，由第10.5节的讨论知道，单位时间内流体经过流向指定侧的流体总质量
可用曲面积分来表示：
如果是高斯公式(1)中闭区域的边界曲面的外侧，那么公式(1)的右端可解释为单位时间内离开闭区域的流体的总质量。
由于我们假定流体是不可压缩的，且流体是稳定的，故当流体离开时，内部必须有产生流体的“源头”产生出同样多的流体来进行补充。因此，高斯公式左端可解释为分布在内的源头在单位时间内产生的流体的总质量。
为了简便起见，把高斯公式(1)改写成
以闭区域的体积
除上式两端，得
上式左端表示内的源头在单位时间单位体积内所产生的流体质量的平均值。应用积分中值定理于上式左端，得
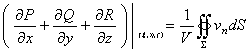
这里
是内的某个点。
令缩向一点
，对上式取极限，得
上式左端称为
在点
的散度，记作
，即
在这里可看作稳定流动的不可压缩流体在点的源头强度 — 单位时间单位体积内所产生的流体质量。如果为负，表示点处流体在消失。
一般地，设某向量场由
给出，其中、、具有一阶连续偏导，是场内的一片有向曲面，
是上点处的单位法向量，则
叫做向量场
通过曲面向着指定侧的通量(或流量)，而
叫做向量场的散度，记作
，即
高斯公式现在可写成
其中是空间闭区域的边界曲面，而
是向量在曲面的外侧法向量上的投影。