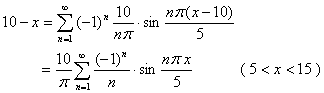§11.10 周期为
对于周期为![]() 的周期函数的傅立叶级数展开,根据已有的结论,借助变量替换,可得到下面定理。
的周期函数的傅立叶级数展开,根据已有的结论,借助变量替换,可得到下面定理。
【定理】设周期为![]() 的周期函数
的周期函数![]() 满足收敛定理的条件,则它的傅立叶级数展开式为
满足收敛定理的条件,则它的傅立叶级数展开式为
![]()
其中系数的计算式为
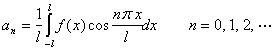

如果![]() 为奇函数,则有
为奇函数,则有
![]()
其中系数 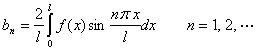
如果![]() 为偶函数,则有
为偶函数,则有
![]()
其中系数 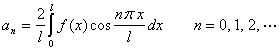
证:作变量替换![]() ,当
,当![]() 时,
时,![]() ,函数
,函数![]() 可重新表示成
可重新表示成![]() ,从而
,从而![]() 是周期为
是周期为![]() 的周期函数且满足收敛定理的条件,因此,
的周期函数且满足收敛定理的条件,因此,![]() 可以展开成为傅立叶级数
可以展开成为傅立叶级数
![]()
其傅立叶系数的计算表达式为
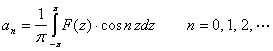
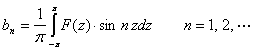
由于![]() ,
,![]() ,上式可分别改写成
,上式可分别改写成
![]()
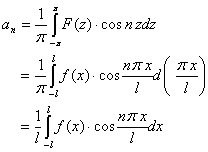
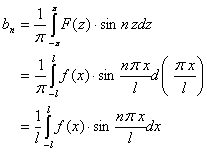
类似地,可以证明定理的其余部分。
【例1】设![]() 是周期为
是周期为![]() 的周期函数,它在
的周期函数,它在![]() 上的表达式为
上的表达式为
![]()
将它展开成傅立叶级数。
解:![]() 的图象如下:
的图象如下:

其傅立叶系数为

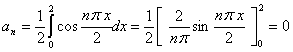
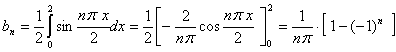
据收敛定理,有

因此,![]() 的傅立叶展开式为
的傅立叶展开式为
![]()
这里,![]()
【例2】将函数![]() 展开成正弦级数和余弦级数。
展开成正弦级数和余弦级数。
解:将![]() 作奇延拓,得到函数
作奇延拓,得到函数![]() ,且
,且
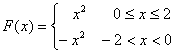
再将![]() 以4为周期进行周期延拓,便可获到一个以4为周期的周期函数,其图象如下:
以4为周期进行周期延拓,便可获到一个以4为周期的周期函数,其图象如下:
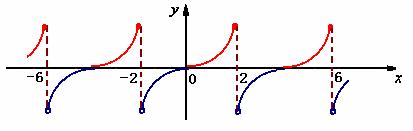
其傅立叶系数为
![]()

由于函数在![]() 处间断,故
处间断,故![]() 的正弦级数展开式为
的正弦级数展开式为
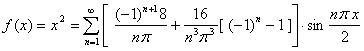
这里: ![]()
再将![]() 作偶延拓,得到函数
作偶延拓,得到函数![]() ,且
,且
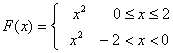
将![]() 以4为周期进行周期延拓,便可获到一个以4为周期的周期函数,其图象如下:
以4为周期进行周期延拓,便可获到一个以4为周期的周期函数,其图象如下:

其傅立叶系数为
![]()
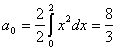
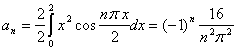
由于函数在![]() 上连续,故
上连续,故![]() 的余弦级数展开式为
的余弦级数展开式为
![]()
这里: ![]()
如果令![]() ,得
,得
![]()
![]()
对定义在任意区间![]() 上的函数
上的函数![]() ,若它满足收敛定理所要求的条件,也可将它展开成傅立叶级数,其方法如下:
,若它满足收敛定理所要求的条件,也可将它展开成傅立叶级数,其方法如下:
作变量替换
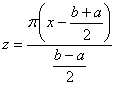 ,即
,即 ![]() ,
,
当![]() 时,
时,![]() ,将函数
,将函数![]() 改写成
改写成
![]()
则![]() 是定义在
是定义在![]() 上,且满足收敛定理条件的函数,从而可将其展开成傅立叶级数。
上,且满足收敛定理条件的函数,从而可将其展开成傅立叶级数。
【例3】将函数![]() 展开成傅立叶级数。
展开成傅立叶级数。
解:作变量替换
![]() ,当
,当![]() 时,则
时,则 ![]() ,而
,而
![]()
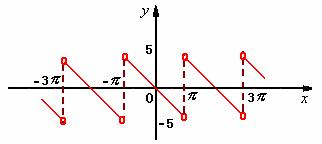
将![]() 以
以![]() 为周期进行周期延拓,可得到一个周期函数,其图象如下:
为周期进行周期延拓,可得到一个周期函数,其图象如下:
其傅立叶系数为
![]()
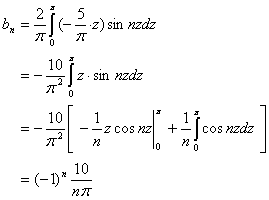
显然,点![]() 是函数的间断点,函数在其它点均连续,故
是函数的间断点,函数在其它点均连续,故![]() 的傅立叶展开式为
的傅立叶展开式为
![]()
将![]() 代入上式,得
代入上式,得