§11.1 常数顶级数的概念和性质

一、级数的定义

若给定一个数列 ，由它构成的表达式

(1)

称之为常数项无穷级数，简称级数，记作。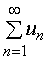

亦即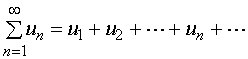

其中第项叫做级数的一般项。

上述级数定义仅仅只是一个形式化的定义，它未明确无限多个数量相加的意义。无限多个数量的相加并不能简单地认为是一项一项地累加起来，因为，这一累加过程是无法完成的。

为给出级数中无限多个数量相加的数学定义，我们引入部分和概念。

作级数(1)的前项之和

(2)

称为级数(1)的部分和。当依次取时，它们构成一个新数列

称此数列为级数(1)的部分和数列。

根据部分和数列(2)是否有极限，我们给出级数(1)收敛与发散的概念。

【定义】当无限增大时，如果级数(1)的部分和数列(2)有极限，即

则称级数(1)收敛，这时极限叫做级数(1)的和，并记作

；

如果部分和数列(2)无极限，则称级数(1)发散。

当级数(1)收敛时，其部分和是级数和的近似值，它们之间的差值

叫做级数的余项。

【注明】由级数定义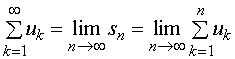发现，它对加法的规定是：依数列的序号大小次序进行逐项累加，因此，级数的敛散性与这种加法规定的方式有关。

【著名反例】

(1)、若逐项相加，部分和为

,

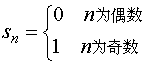无极限，故级数发散。

(2)、若每两项相加之后再各项相加，有

【例1】讨论等比级数

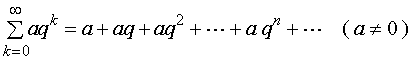
的敛散性。

解：若，则部分和为

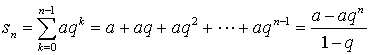
(1)、当时，，故，

等比级数收敛，且和为；

(2)、当时，，从而，

等比级数发散；

(3)、当时，

若，则

若， 则

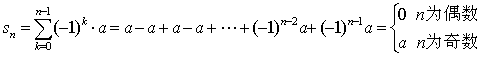
不存在。

即当时，等比级数发散。

综合有

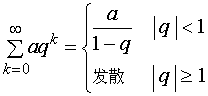
【例2】研究下列伸缩型级数的敛散性

1、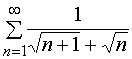

2、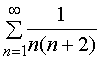

解1、

从而

因此，级数1是发散的。

解2、

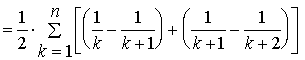
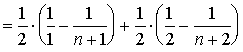
从而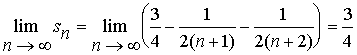

因此，级数2收敛于。

二、级数的基本性质

【性质一】如果级数

收敛于和，则它的各项同乘以一个常数所得的级数

也收敛，且和为。

【证明】设与的部分和分别为、，则

于是，

故级数收敛且和为。

由关系式 ，有

如果没有极限，且，那未也没有极限。

因此，我们得到如下重要结论

级数的每一项同乘一个不为零的常数后，它的敛散性不变。

【性质二】设有级数

分别收敛于与， 则级数

也收敛，且和为。

【证明】设级数、的部分和分别为、， 则部分和

故

这表明级数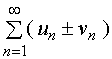收敛且其和为。

据性质二，我们可得到几个有用的结论

1、若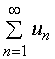与收敛，则

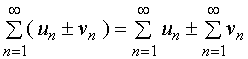(分配律)

(一种结合律)

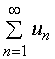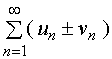2、若收敛，而发散，则必发散。

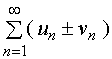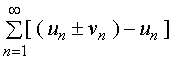反证：假设收敛，则亦收敛，

即收敛，这与条件相矛盾。

3、若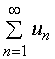、均发散，那么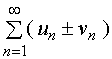可能收敛，也可有发散。

如 ，

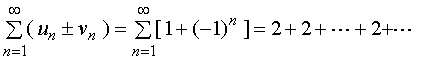发散

又如 ，

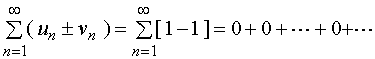收敛

【性质三】在级数的前面去掉或加上有限项，不会影响级数的敛散性，不过在收敛时，一般来说级数的和是要改变的。

【证明】将级数

的前项去掉，得到新级数

新级数的部分和为

其中是原级数前项的部分和，而是原级数前项之和(它是一个常数)。故当时，与具有相同的敛散性。在收敛时，其收敛的和有关系式

其中 ，，

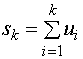
类似地，可以证明在级数的前面增加有限项，不会影响级数的敛散性。

【性质四】将收敛级数的某些项加括号之后所成新级数仍收敛于原来的和。

【证明】设有收敛级数

它按照某一规律加括号后所成的级数为

用表示这一新级数的前项之和，它是由原级数中前项之和所构成的()，即有

显然，当时，有，因此

级数加括号与去括号之后所得新级数的敛散性较复杂，下列事实在解题中会常用到。

1、如果级数加括号之后所形成的级数发散，则级数本身也一定发散。

显然，这是性质四的逆否命题。

2、收敛的级数去括号之后所成级数不一定收敛。

例如，级数收敛于零，但去括号之后所得级数

却是发散的。

这一事实也可以反过来陈述：

即使级数加括号之后收敛，它也不一定就收敛。

三、级数收敛的必要条件

对于级数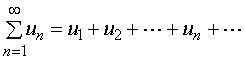

它的一般项与部分和有关系式

假设该级数收敛于和，则

于是，我们有如下级数收敛的必要条件。

【定理】级数收敛的必要条件是。

必须指出，级数的一般项趋向于零并不是级数收敛的充分条件。

【著名反例】讨论调和级数

的敛散性。

这里，，即调和级数的一般项趋近于零。

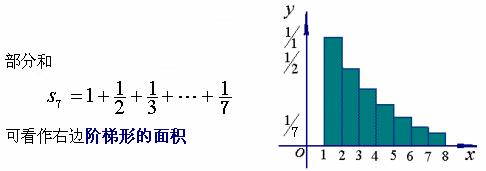
考虑由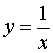，，，轴所围成的曲边梯形的面积与这个阶梯形面积的关系。

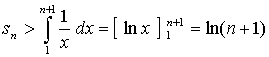
当时，，从而，

因此，调和级数发散到。