§11.2
常数项级数的审敛法
一、正项级数及审敛法
若级数![]() 中的各项都是非负的( 即
中的各项都是非负的( 即![]() ),则称级数
),则称级数![]() 为正项级数。
为正项级数。
由于级数的敛散性可归结为正项级数的敛散性问题,因此,正项级数的敛散性判定就显得十分地重要。
1、基本定理
正项级数收敛的充要条件是它的部分和数列有界。
【证明】设级数
![]() (1)
(1)
是一个正项级数,它的部分和数列
![]()
是单调增加的,即
![]() 。
。
若数列![]() 有上界
有上界![]() ,据单调有界数列必有极限的准则,级数(1)必收敛于和
,据单调有界数列必有极限的准则,级数(1)必收敛于和![]() ,且
,且![]() 。
。
反过来,如果级数(1)收敛于和![]() ,即
,即![]() ,据极限存在的数列必为有界数列性质可知,部分和数列
,据极限存在的数列必为有界数列性质可知,部分和数列![]() 是有界的。
是有界的。
2、基本审敛法
借助正项级数收敛的基本定理,我们来建立一系列具有实用性的正项级数审敛法。
【比较审敛法】给定两个正项级数![]() 、
、![]()
(1)、若![]() ,而
,而![]() 收敛,则
收敛,则![]() 亦收敛;
亦收敛;
(2)、若![]() ,而
,而![]() 发散,则
发散,则![]() 亦发散。
亦发散。
这里,级数![]() 称作级数
称作级数![]() 的比较级数。
的比较级数。
【证明】(1) 设![]() 收敛于
收敛于![]() ,
,
由![]() ,
,![]() 的部分和
的部分和![]() 满足
满足
![]()
即单调增加的部分和数列![]() 有上界。
有上界。
据基本定理知,![]() 收敛。
收敛。
(2) 设![]() 发散,于是它的部分和
发散,于是它的部分和
![]()
由![]() ,有
,有
![]()
从而 ![]() ,即
,即![]() 发散。
发散。

由于级数的每一项同乘以一个非零常数![]() ,以及去掉其有限项不会影响它的敛散性,比较审敛法可改写成如下形式
,以及去掉其有限项不会影响它的敛散性,比较审敛法可改写成如下形式
【推论】设![]() 为正数,
为正数,![]() 为正整数,
为正整数,![]() 、
、![]() 均为正项级数
均为正项级数
(1)、若![]() ,而
,而![]() 收敛,则
收敛,则![]() 亦收敛;
亦收敛;
(2)、若![]() ,而
,而![]() 发散,则
发散,则![]() 亦发散。
亦发散。
【例1】讨论 ![]() 级数
级数

的敛散性,其中![]() 。
。
【解】1、若![]() ,则
,则 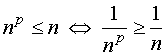 ,而调和级数
,而调和级数![]() 发散,
发散,
故 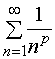 亦发散;
亦发散;
2、若![]() ,对于
,对于 ![]() ,有
,有
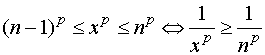 ,
,
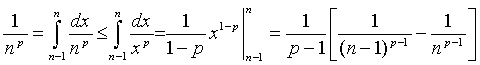
考虑比较级数
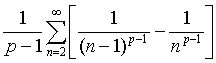
它的部分和
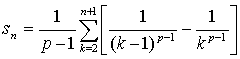
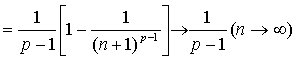
故
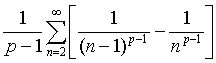 收敛,由比较审敛法,
收敛,由比较审敛法,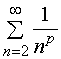 收敛,
收敛,
由级数的性质,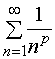 亦收敛。
亦收敛。
综上讨论,当
![]() 时,
时,![]() 级数为发散的;
级数为发散的;
当 ![]() 时,
时,![]() 级数是收敛的。
级数是收敛的。
![]() 级数是一个重要的比较级数,在解题中会经常用到。
级数是一个重要的比较级数,在解题中会经常用到。
比较审敛法还可用其极限形式给出,而极限形式在运用中更显得方便。
【比较审敛法的极限形式】
设![]() 及
及![]() 为两个正项级数,如果极限
为两个正项级数,如果极限
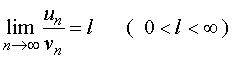
则级数![]() 与
与![]() 同时收敛或同时发散。
同时收敛或同时发散。
【证明】由极限的定义有
对![]() ,存在着自然数
,存在着自然数![]() ,当
,当![]() 时,有不等式
时,有不等式
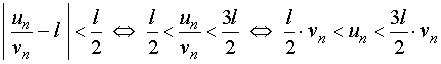
再据比较审敛法的推论,即获得了要证的结论。
![]()
【极限审敛法】设![]() 为正项级数,
为正项级数,
(1)、若![]() ,则
,则![]() 发散;
发散;
(2)、若![]() ,则
,则![]() 收敛。
收敛。
【证明】若 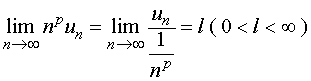
故
![]() 与
与 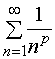 具有相同的收敛性,亦即
具有相同的收敛性,亦即
(1)、当![]() 时,
时,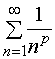 收敛,故
收敛,故![]() 收敛;
收敛;
(2)、当![]() 时,
时,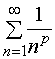 发散,故
发散,故![]() 发散;
发散;
(3)、![]()
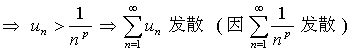
(4)、![]()
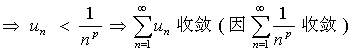
【例2】判别级数
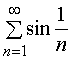 、
、

的敛散性。
解: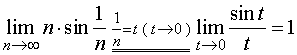
故级数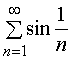 发散;
发散;
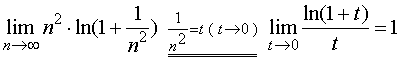
故级数 收敛。
收敛。
![]()
【比值审敛法】
若正项级数![]() 适合
适合
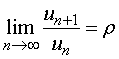
则Ê当![]() 时,级数收敛;
时,级数收敛;
Ë当![]() (也包括
(也包括![]() )时,级数发散;
)时,级数发散;
Ì当![]() 时,级数的敛散性不详。
时,级数的敛散性不详。
【证明】
Ê当![]() 时,可取一适合小的正数
时,可取一适合小的正数![]() ,使得
,使得 ![]()
据极限的定义,存在自然数![]() ,当
,当![]() 时,
时,
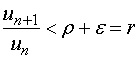 ,
,![]()
有 ![]()
![]()
![]() ,…
,…
级数![]() 的各项小于收敛的等比级数(
的各项小于收敛的等比级数(![]() )
)
![]()
的对应项,故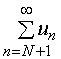 收敛,从而
收敛,从而![]() 亦收敛;
亦收敛;
Ë当![]() 时,
时,
存在充分小的正数![]() ,使得
,使得![]() ,据极限定义,当
,据极限定义,当![]() 时,有
时,有
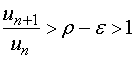 ,
,![]()
因此,当![]() 时,级数的一般项是逐渐增大的,它不趋向于零,
时,级数的一般项是逐渐增大的,它不趋向于零,
由级数收敛的必要条件,![]() 发散。
发散。
Ì当![]() 时,级数可能收敛,也可能发散。
时,级数可能收敛,也可能发散。
例如,对于![]() 级数
级数 ,不论
,不论![]() 取何值,总有
取何值,总有
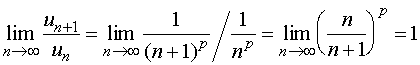
但是,级数在![]() 时收敛,而当
时收敛,而当![]() 时,它是发散。
时,它是发散。
【根值审敛法】
若正项级数![]() 适合
适合
![]()
则Ê当![]() 时,级数收敛;
时,级数收敛;
Ë当![]() (也包括
(也包括![]() )时,级数发散;
)时,级数发散;
Ì当![]() 时,级数的敛散性不详。
时,级数的敛散性不详。
【证明】
Ê当![]() 时,可取一适合小的正数
时,可取一适合小的正数![]() ,使得
,使得 ![]()
据极限的定义,存在自然数![]() ,当
,当![]() 时,
时,
![]() ,
,![]()
等比级数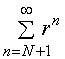 (
(![]() )是收敛的,因此
)是收敛的,因此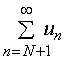 亦收敛,
亦收敛,
故级数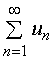 收敛。
收敛。
Ë当![]() 时,
时,
存在充分小的正数![]() ,使得
,使得![]() ,据极限定义,当
,据极限定义,当![]() 时,有
时,有
![]() ,
,![]()
因此,级数的一般项不趋向于零,由级数收敛的必要条件,![]() 发散。
发散。
Ì当![]() 时,级数可能收敛,也可能发散。
时,级数可能收敛,也可能发散。
例如,级数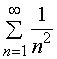 是收敛,级数
是收敛,级数![]() 是发散的,而
是发散的,而
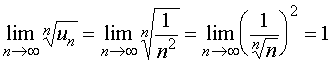
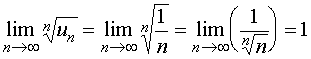
对于比值法与根值法失效的情形(![]() ),其级数的敛散性应加另寻它法加以判定,通常是构造更精细的比较级数。
),其级数的敛散性应加另寻它法加以判定,通常是构造更精细的比较级数。
【例3】判定下列级数的敛散性
1、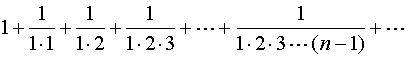
2、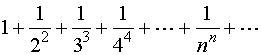
3、
解:1、一般项为 

由比值审敛法知,级数1是收敛的。
2、一般项为 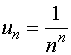
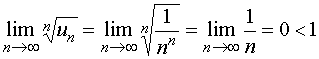
由根值审敛法知,级数2是收敛的。
3、一般项为 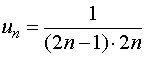

这表明,用比值法无法确定该级数的敛散性。注意到

而级数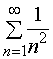 收敛,由比较判别法,级数3收敛。
收敛,由比较判别法,级数3收敛。
二、交错级数及其审敛法
所谓交错级数是这样的级数,它的各项是正、负交错的,其形式如下
![]() (1)
(1)
或 ![]()
其中![]() 均为正数。
均为正数。
【交错级数审敛法】(又称莱布尼兹定理)
如果交错级数(1)满足条件
Ê ![]()
Ë ![]()
则交错级数(1)收敛,且收敛和![]() ,余项
,余项![]() 的绝对值
的绝对值![]() 。
。
【证明】
1、先证![]() 存在。
存在。
将(1)式的前![]() 项的部分和
项的部分和![]() 写成如下两种形式
写成如下两种形式
![]()
及 ![]()
由条件(1) ![]() 可知
可知
所有括号内的差均非负,第一个表达式表明:数列![]() 是单调增加的;而第二个表达式表明:
是单调增加的;而第二个表达式表明:![]() ,数列
,数列![]() 有上界。
有上界。
由单调有界数列必有极限准则,当![]() 无限增大时,
无限增大时,![]() 趋向于某值
趋向于某值![]() ,并且
,并且![]() 。
。
即 ![]()
2、再证![]()
因
![]()
由条件(2) ![]() 可知,
可知,
![]()
由于级数的偶数项之和与奇数项之和都趋向于同一极限,故级数(1)的部分和当![]() 时具有极限
时具有极限![]() 。这就证明了级数(1)收敛于
。这就证明了级数(1)收敛于![]() ,且
,且![]() 。
。
3、最后证明![]()
余项可以写成
![]()
其绝对值为 ![]()
此式的右端也是一个交错级数,它满足收敛的两个条件,故其和应小于它的首项,即
![]()
【例4】试证明交错级数
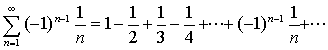
是收敛的。
【证明】
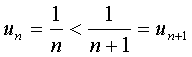
且 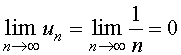
故此交错级数收敛,并且和![]() 。
。
三、绝对收敛与条件收敛
设有级数 ![]() (2)
(2)
其中![]() 为任意实数,该级数称为任意项级数。
为任意实数,该级数称为任意项级数。
下面,我们考虑级数(2)各项的绝对值所组成的正项级数
![]() (3)
(3)
的敛散性问题。
【定义】
如果级数(3)收敛,则称级数(2)绝对收敛;
如果级数(3)发散,而级数(2)收敛,则称级数(2)条件收敛。
【定理一】如果级数(3)收敛,则级数(2)亦收敛。
【证明】设级数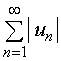 收敛
收敛
令
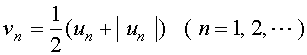
显然
![]() , 且
, 且 ![]()
而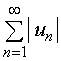 收敛,由比较审敛法,正项级数
收敛,由比较审敛法,正项级数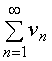 收敛,
收敛,
从而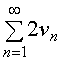 亦收敛,另一方面,
亦收敛,另一方面,![]()
由级数性质,级数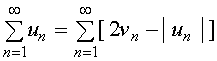 收敛。
收敛。
定理一将任意项级数的敛散性判定转化成正项级数的收敛性判定。
【例6】判定任意项级数 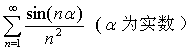 的收敛性。
的收敛性。
解因 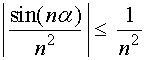
而 收敛,故
收敛,故 亦收敛,
亦收敛,
据定理一,级数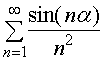 收敛。
收敛。
【例7】讨论级数 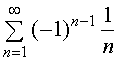 的收敛性。
的收敛性。
解 因调和级数![]() 发散,
发散,
而交错级数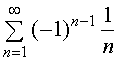 收敛,
收敛,
故级数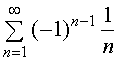 非绝对收敛,仅仅是条件收敛的。
非绝对收敛,仅仅是条件收敛的。
由定理一与例三,可总结出绝对收敛、条件收敛与收敛之间的关系。

有限项相加的重要性质之一是其和与相加的次序无关(即加法具有交换律、结合律)。这样的性质可否搬到无穷级数呢?
无穷级数一般不具备这样的性质,即使是条件收敛的级数也不具备有这样的性质。但如果级数绝对收敛,则级数中的各项可任意地改变位置(即交换律成立)、可任意地添加括号(即结合律成立)。
【定理二】如果级数
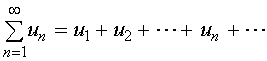
绝对收敛,其和为![]() ,那么任意颠倒级数各项的顺序所得到的新级数
,那么任意颠倒级数各项的顺序所得到的新级数

仍绝对收敛,且其和仍为![]() 。
。
【典型例子】交错级数

条件收敛,设它的收敛和为![]() 。
。
下面讨论它的几种新组合
1、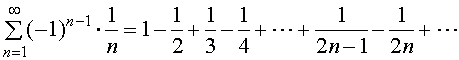
它的前![]() 项所作成的部分和为
项所作成的部分和为
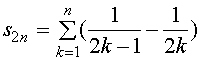
对级数的项作如下重排
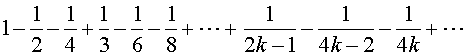 (4)
(4)
它的前![]() 项所作成的部分和为
项所作成的部分和为


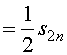
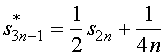 ,
, 
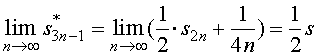
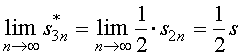
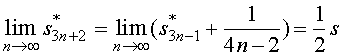
这表明,重排之后的新级数收敛于![]() 。
。
2、对级数的项作如下重排
![]()
它的前![]() 项部分和为
项部分和为
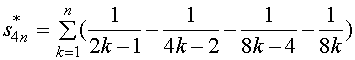
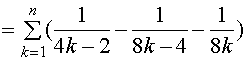

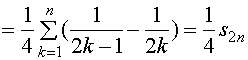
而 
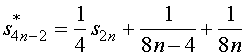
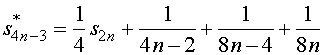
![]()
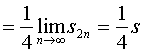
故,重排之后的新级数收敛于![]() 。
。
由1、2可知,级数重排后,改变了级数的收敛和。因此,非绝对收敛的级数不能进行项的重排。