§11.4
幂级数
一、函数项级数的一般概念
设有定义在区间 ![]() 上的函数列
上的函数列
![]()
由此函数列构成的表达式
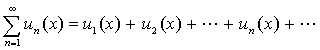 (1)
(1)
称作函数项级数。
对于确定的值![]() ,函数项级数(1)成为常数项级数
,函数项级数(1)成为常数项级数
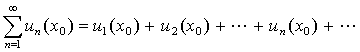 (2)
(2)
若(2)收敛,则称点![]() 是函数项级数(1)的收敛点;
是函数项级数(1)的收敛点;
若(2)发散,则称点![]() 是函数项级数(1)的发散点;
是函数项级数(1)的发散点;
函数项级数的所有收敛点的全体称为它的收敛域;
函数项级数的所有发散点的全体称为它的发散域。
对于函数项级数收敛域内任意一点![]() ,(1)收敛, 其收敛和自然应依赖于
,(1)收敛, 其收敛和自然应依赖于![]() 的取值,故其收敛和应为
的取值,故其收敛和应为![]() 的函数,即为
的函数,即为![]() 。通常称
。通常称![]() 为函数项级数的和函数。它的定义域就是级数的收敛域,并记
为函数项级数的和函数。它的定义域就是级数的收敛域,并记
![]()
若将函数项级数(1)的前![]() 项之和(即部分和)记作
项之和(即部分和)记作![]() ,则在收敛域上有
,则在收敛域上有 ![]()
若把![]() 叫做函数项级数的余项(这里
叫做函数项级数的余项(这里![]() 在收敛域上),则
在收敛域上),则 ![]() 。
。
二、幂级数及其收敛域
函数项级数中最常见的一类级数是所谓幂级数,它的形式是
![]() (3)
(3)
或 ![]() (4)
(4)
其中常数![]() 称作幂级数系数。
称作幂级数系数。
(4)式是幂级数的一般形式,作变量代换![]() 可以把它化为(3)的形式。
可以把它化为(3)的形式。
因此,在下述讨论中,如不作特殊说明,我们用幂级数(3)式作为讨论的对象。
1、幂级数的收敛域、发散域的构造
先看一个著名的例子,考察等比级数( 显然也是幂级数 )
![]()
的收敛性。
当![]() 时,该级数收敛于和
时,该级数收敛于和![]() ;
;
当![]() 时,该级数发散。
时,该级数发散。
因此,该幂级数的收敛域是开区间![]() ,发散域是
,发散域是![]() 及
及![]() ,如果在开区间
,如果在开区间![]() 内取值,则
内取值,则
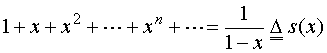
由此例,我们观察到,这个幂级数的收敛域是一个区间。事实上,这一结论对一般的幂级数也是成立的。
【定理一】(阿贝尔定理)
若![]() 时,幂级数
时,幂级数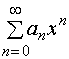 收敛,则适合不等式
收敛,则适合不等式![]() 的一切
的一切![]() 均使幂级数绝对收敛;
均使幂级数绝对收敛;
若![]() 时,幂级数
时,幂级数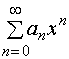 发散,则适合不等式
发散,则适合不等式![]() 的一切
的一切![]() 均使幂级数发散。
均使幂级数发散。
【证明】先设![]() 是幂级数
是幂级数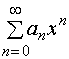 的收敛点, 即级数
的收敛点, 即级数
![]()
收敛,则
![]() 。
。
于是存在一个正数![]() ,使得
,使得
![]()
从而
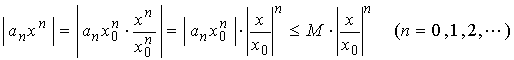
当![]() 时,
时, ,等比级数
,等比级数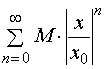 收敛,从而
收敛,从而
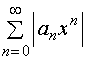 收敛,故幂级数
收敛,故幂级数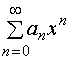 绝对收敛;
绝对收敛;
定理一的第二部分可用反证法证明
假设幂级数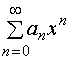 当
当![]() 时发散,而有一点
时发散,而有一点![]() 适合
适合![]() 使级数收敛。
使级数收敛。
据定理一的第一部分,级数当![]() 时应收敛,这与定理的条件相矛盾,故定理的第二部分应成立。
时应收敛,这与定理的条件相矛盾,故定理的第二部分应成立。
阿贝尔定理揭示了幂级数的收敛域与发散域的结构
对于幂级数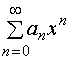
若在![]() 处收敛,则在开区间
处收敛,则在开区间![]() 之内,它亦收敛;
之内,它亦收敛;
若在![]() 处发散,则在开区间
处发散,则在开区间![]() 之外,它亦发散;
之外,它亦发散;
这表明,幂级数的发散点不可能位于原点与收敛点之间。
于是,我们可以这样来寻找幂级数的收敛域与发散域
设幂级数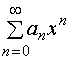 在数轴上既有收敛点(不仅仅只是原点,原点肯定是一个收敛点),也有发散点。
在数轴上既有收敛点(不仅仅只是原点,原点肯定是一个收敛点),也有发散点。
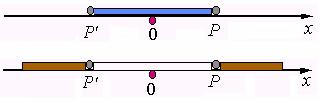
Œ从原点出发,沿数轴向右方搜寻,最初只遇到收敛点,然后就只遇到发散点,设这两部分的界点为P,点P可能是收敛点,也可能是发散点;
从原点出发,沿数轴向左方搜寻,情形也是如此,也可找到一个界点P’,两个界点在原点的两侧,由定理一知,它们到原点的距离是一样的。
Ž位于点P’与P之间的点,就是幂级数的收敛域;位于这两点之外的点,就是幂级数的发散域。
借助上述几何解释,我们就得到如下重要推论
【推论】如果幂级数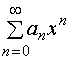 不是仅在一点收敛,也不是在整个数轴上都收敛,则必有一个确定的正数
不是仅在一点收敛,也不是在整个数轴上都收敛,则必有一个确定的正数![]() 存在,它具有下列性质
存在,它具有下列性质
Œ当![]() 时,幂级数绝对收敛;
时,幂级数绝对收敛;
当![]() 时,幂级数发散;
时,幂级数发散;
Ž当![]() 时,幂级数可能收敛,也可能发散。
时,幂级数可能收敛,也可能发散。
正数![]() 通常称作幂级数的收敛半径。
通常称作幂级数的收敛半径。

由幂级数在![]() 处的敛散性就可决定它在区间
处的敛散性就可决定它在区间![]() ,
,![]() ,
,![]() 或
或![]() 上收敛,这区间叫做幂级数的收敛区间。
上收敛,这区间叫做幂级数的收敛区间。
特别地,如果幂级数只在![]() 处收敛,则规定收敛半径
处收敛,则规定收敛半径![]() ;如果幂级数对一切
;如果幂级数对一切![]() 都收敛,则规定收敛半径
都收敛,则规定收敛半径![]() 。
。
2、幂级数的收敛半径的求法
【定理二】设有幂级数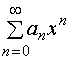 ,且
,且
 (
(![]() ,
,![]() 是幂级数的相邻两项的系数)
是幂级数的相邻两项的系数)
如果 Œ![]() ,则
,则 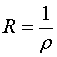 ;
;
![]() ,则
,则 ![]() ;
;
Ž![]() ,则
,则 ![]() 。
。
【证明】考察幂级数的各项取绝对值所成的级数
![]() (*)
(*)
该级数相邻两项之比为 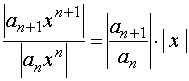
若 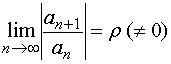 存在,据比值审敛法,
存在,据比值审敛法,
Œ当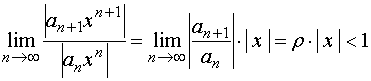
即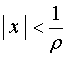 时,级数(*)收敛,从而原幂级数绝对收敛;
时,级数(*)收敛,从而原幂级数绝对收敛;
当![]() ,即
,即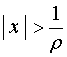 时,级数(*)从某个
时,级数(*)从某个![]() 开始,有
开始,有
![]()
从而![]() 不趋向于零,进而
不趋向于零,进而 ![]() 也不趋向于零,因此原幂级数发散。
也不趋向于零,因此原幂级数发散。
于是,收敛半径 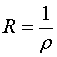 ;
;
‚若![]() ,则对任何
,则对任何![]() ,有
,有
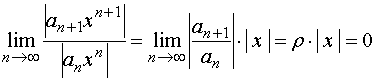
从而级数(*)收敛,原幂级数绝对收敛
于是,
收敛半径 ![]() ;
;
ƒ若![]() ,则对任何
,则对任何![]() ,有
,有
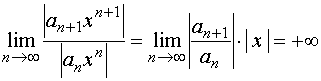
依极限理论知,从某个![]() 开始有
开始有
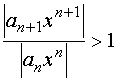 ,
,![]()
因此 ![]() ,
,
从而 ![]()
原幂级数发散。
于是,收敛半径![]() 。
。
【例1】求下列幂级数的收敛半径与收敛区间
1、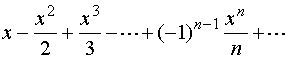
2、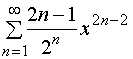
解1:这里

![]()
在左端点![]() ,幂级数成为
,幂级数成为
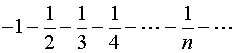
它是发散的;
在右端点![]() ,幂级数成为
,幂级数成为
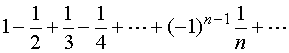
它是收敛的。
收敛区间为![]() 。
。
解2.此幂级数缺少奇次幂项,可据比值审敛法的原理来求收敛半径
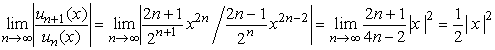
当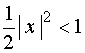 ,即
,即![]() 时,幂级数收敛;
时,幂级数收敛;
当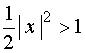 ,即
,即![]() 时,幂级数发散;
时,幂级数发散;
对于左端点![]() ,幂级数成为
,幂级数成为
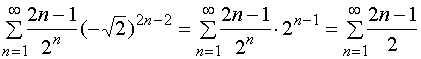
它是发散的;
对于右端点![]() ,幂级数成为
,幂级数成为
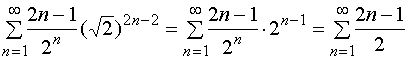
它也是发散的。
故收敛区间为
![]() 。
。
【例2】求函数项级数的收敛域
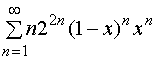
解:作变量替换 ![]() ,则函数项级数变成了幂级数
,则函数项级数变成了幂级数
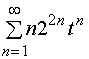
因
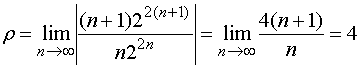
故收敛半径为 。
。
在左端点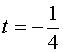 ,幂级数成为
,幂级数成为

它是发散的;
在右端点![]() ,幂级数成为
,幂级数成为
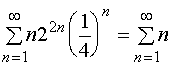
它也是发散的。
故收敛区间为
 。
。
即 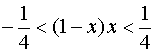 ,
,
亦即 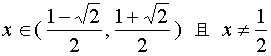 。
。
三 幂级数的运算性质
对下述性质,我们均不予以证明
1.加,减运算
设幂级数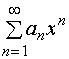 及
及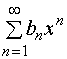 的收敛区间分别为
的收敛区间分别为![]() 与
与![]() ,记
,记![]() ,当
,当![]() 时,有
时,有

2.幂级数和函数的性质
Ê幂级数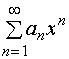 的和函数
的和函数![]() 在收敛区间
在收敛区间![]() 内连续。
内连续。
Ë若幂级数在敛区的左端点![]() 收敛,则其和函数
收敛,则其和函数![]() 在
在![]() 处右连续,即
处右连续,即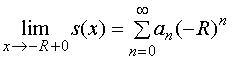 ;
;
Ì若幂级数在敛区的右端点 ![]() 处收敛,则其和函数
处收敛,则其和函数![]() 在
在![]() 处左连续,即
处左连续,即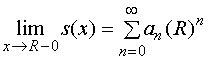 。
。
注:这一性质在求某些特殊的数项级数之和时, 非常有用。
3.逐项求导
幂级数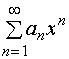 的和函数
的和函数![]() 在收敛区间
在收敛区间![]() 内可导,且有
内可导,且有
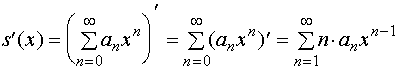
4.逐项求积分
幂级数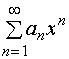 的和函数
的和函数![]() 在收敛区间
在收敛区间![]() 内可积,且有
内可积,且有
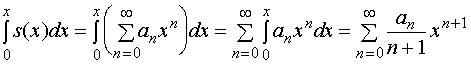

【例3】求数项级数 之和。
之和。
解: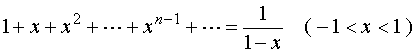
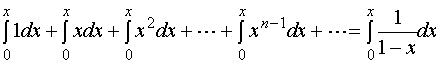
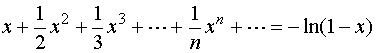
当![]() 时,幂级数成为
时,幂级数成为
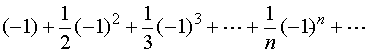
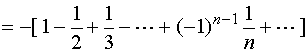
是一收敛的交错级数。
当![]() 时,幂级数成为
时,幂级数成为
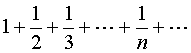
是发散的调和级数。
故 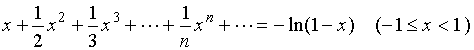
且有 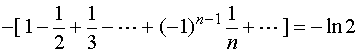

【例4】求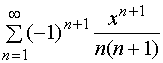 的和函数。
的和函数。
解: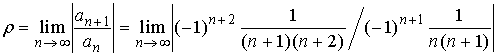
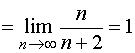
![]()
设
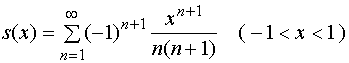
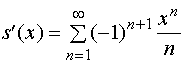
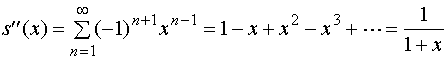
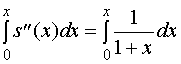
![]()
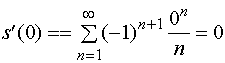
![]()
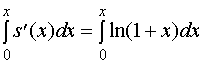
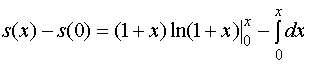
![]()
当![]() 时,幂级数成为
时,幂级数成为

它是收敛的;
当![]() 时,幂级数成为
时,幂级数成为
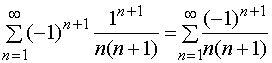
它是收敛的;
因此,当
![]() 时,有
时,有
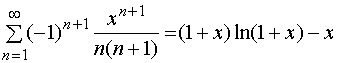
【例5】求 的和。
的和。
解:考虑辅助幂级数 ![]()

![]()
设
![]()
![]()
![]()
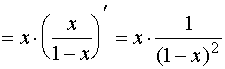
故,当
![]() 时,有
时,有
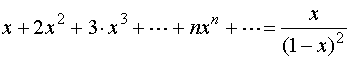
令
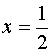 ,得
,得