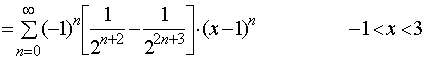§11.5
函数展开成幂级数
一、泰勒级数
如果![]() 在
在![]() 处具有任意阶的导数,我们把级数
处具有任意阶的导数,我们把级数
![]() (1)
(1)
称之为函数![]() 在
在![]() 处的泰勒级数。
处的泰勒级数。
它的前![]() 项部分和用
项部分和用![]() 记之,且
记之,且
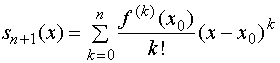
这里:![]()
由上册中介绍的泰勒中值定理,有
![]()
当然,这里![]() 是拉格朗日余项,且
是拉格朗日余项,且
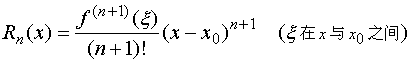 。
。
由![]() 有
有
![]() 。
。
因此,当![]() 时,函数
时,函数![]() 的泰勒级数
的泰勒级数
![]()
就是它的另一种精确的表达式。即
![]()
这时,我们称函数![]() 在
在![]() 处可展开成泰勒级数。
处可展开成泰勒级数。
特别地,当![]() 时,
时,
![]()
这时,我们称函数![]() 可展开成麦克劳林级数。
可展开成麦克劳林级数。
将函数![]() 在
在![]() 处展开成泰勒级数,可通过变量替换
处展开成泰勒级数,可通过变量替换![]() ,化归为函数
,化归为函数 ![]() 在
在 ![]() 处的麦克劳林展开。因此,我们着重讨论函数的麦克劳林展开。
处的麦克劳林展开。因此,我们着重讨论函数的麦克劳林展开。
【命题】函数的麦克劳林展开式是唯一的。
证明:设![]() 在
在![]() 的某邻域
的某邻域![]() 内可展开
内可展开![]() 成的幂级数
成的幂级数
![]()
据幂级数在收敛区间内可逐项求导,有
![]()
![]()
![]()
![]()
![]()
把![]() 代入上式,有
代入上式,有
![]()
![]()
![]()
![]()
![]()
![]()
从而 ![]()

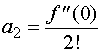
![]()
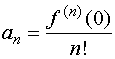
![]()
于是,函数![]() 在
在![]() 处的幂级数展开式其形式为
处的幂级数展开式其形式为
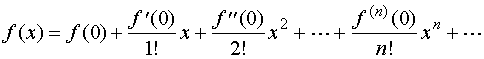
这就是函数的麦克劳林展开式。
这表明,函数在![]() 处的幂级数展开形式只有麦克劳林展开式这一种形式。
处的幂级数展开形式只有麦克劳林展开式这一种形式。
二、函数展开成幂级数
1、直接展开法
将函数展开成麦克劳林级数可按如下几步进行
Œ求出函数的各阶导数及函数值
![]()
若函数的某阶导数不存在,则函数不能展开;
写出麦克劳林级数

并求其收敛半径![]() 。
。
Ž考察当![]() 时,拉格朗日余项
时,拉格朗日余项
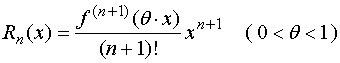
当![]() 时,是否趋向于零。
时,是否趋向于零。
若![]() ,则第二步写出的级数就是函数的麦克劳林展开式;
,则第二步写出的级数就是函数的麦克劳林展开式;
若![]() ,则函数无法展开成麦克劳林级数。
,则函数无法展开成麦克劳林级数。
【例1】将函数![]() 展开成麦克劳林级数。
展开成麦克劳林级数。
解:![]()
于是得麦克劳林级数
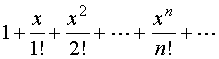
而

故
![]()
对于任意
![]() ,有
,有
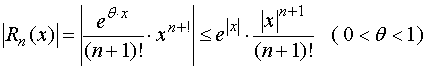
这里![]() 是与
是与![]() 无关的有限数, 考虑辅助幂级数
无关的有限数, 考虑辅助幂级数

的敛散性。
由比值法有

故辅助级数收敛,从而一般项趋向于零,即 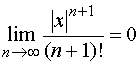
因此 ![]() ,故
,故
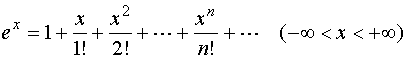
【例2】将函数![]() 在
在![]() 处展开成幂级数。
处展开成幂级数。
解:
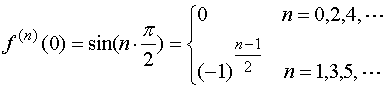
于是得幂级数 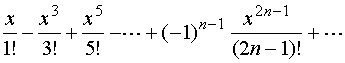
容易求出,它的收敛半径为
![]()
对任意的![]() ,有
,有
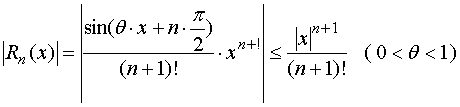
由例一可知,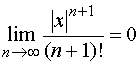 ,故
,故 ![]()
因此,我们得到展开式
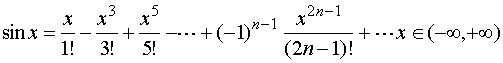

2、间接展开法
利用一些已知的函数展开式以及幂级数的运算性质( 如:加减,逐项求导,逐项求积)将所给函数展开。
【例3】将函数![]() 展开成
展开成![]() 的幂级数。
的幂级数。
解:对展开式
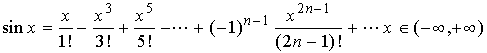
两边关于![]() 逐项求导, 得
逐项求导, 得
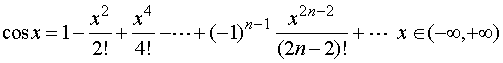
【例4】将函数![]() 展开成
展开成![]() 的幂级数。
的幂级数。
解: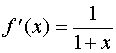
而 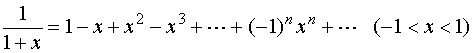
将上式从![]() 到
到![]() 逐项积分得
逐项积分得
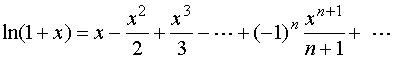
当![]() 时,交错级数
时,交错级数

收敛。
故
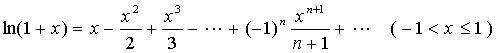

下面,我们介绍十分重要牛顿二项展开式
【例5】将函数![]() 展开成的幂级数,其中
展开成的幂级数,其中![]() 为任意实数。
为任意实数。
解:![]()
![]()
![]()
![]()
![]()
![]()
于是得到幂级数
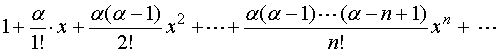
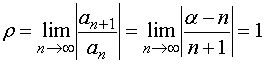
因此,对任意实数![]() ,幂级数在
,幂级数在![]() 内收敛。
内收敛。
下面,我们证明,该幂级数收敛的和函数就是函数![]() 。
。
设上述幂级数在![]() 内的和函数为
内的和函数为![]() ,即
,即
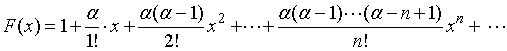
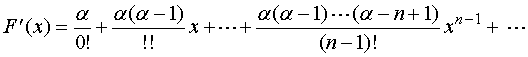
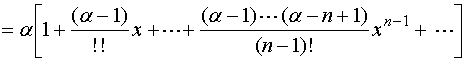
两边同乘以因子![]() ,有
,有
![]()

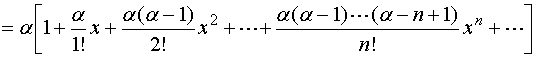
![]()
即 ![]()
引入辅助函数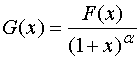
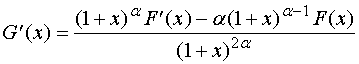
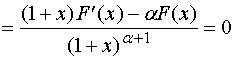
![]()
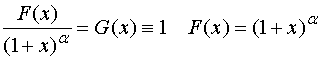
因此,在![]() 内,我们有展开式
内,我们有展开式
![]()
注记
¶在区间端点![]() 处的敛散性,要看实数
处的敛散性,要看实数![]() 的取值而定,这里,我们不作进一步地介绍。
的取值而定,这里,我们不作进一步地介绍。
·若引入广义组合记号 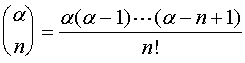 ,牛顿二项展开式可简记成
,牛顿二项展开式可简记成
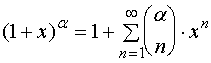
最后,我们举一个将函数展开成![]() 的幂级数形式的例子。
的幂级数形式的例子。
【例6】将函数 展开成
展开成![]() 的幂级数。
的幂级数。
解:作变量替换![]() ,则
,则 ![]() ,有
,有

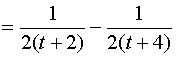
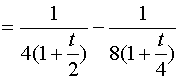
而 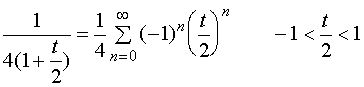
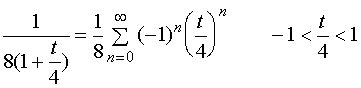
于是