§11.6
函数的幂级数展开式的应用
一、近似计算
利用函数的幂级数展开式,可以进行近似计算。
1、一些近似计算中的术语
Œ误差不超过![]()
设![]() 为精值,而
为精值,而![]() 为近似值,则
为近似值,则![]() 表示
表示![]() 与
与![]() 之间的绝对误差。
之间的绝对误差。

误差不超过![]() (
( ![]() ) 意指:
) 意指:
近似值![]() 与精值
与精值![]() 之差,在小数点后的
之差,在小数点后的![]() 位是完全一样的,仅在小数点后的第
位是完全一样的,仅在小数点后的第![]() 位相差不超过一个单位。
位相差不超过一个单位。
例如:![]() ,
,![]()
![]()
有时,也将误差不超过![]() 说成:精确到小数点后
说成:精确到小数点后![]() 位。
位。
截断误差(或方法误差)
函数![]() 用泰勒多项式
用泰勒多项式

来近似代替,则该数值计算方法的截断误差是
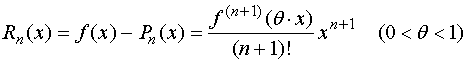
¸舍入误差
用计算机作数值计算,由于计算机的字长有限,原始数据在计算机上表示会产生误差,用这些近似表示的数据作计算,又可能造成新的误差,这种误差称为舍入误差。
例如,用3.14159 近似代替 p,产生的误差
d =p - 3.14159
= 0.0000026L
就是舍入误差。
2、根式计算
【例1】计算![]() 的近似值( 精确到小数四位)。
的近似值( 精确到小数四位)。

求根式的近似值,要选取一个函数的幂级数展开式,可选牛顿二项展开式

要利用此式,需要将![]() 表示成
表示成![]() 的形式,通常当
的形式,通常当![]() 较小时,计算效果会较好。
较小时,计算效果会较好。

这里,可取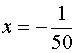 ,
, 。
。
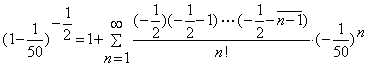

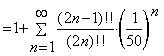
解:利用二项展开式,有
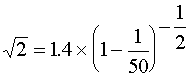
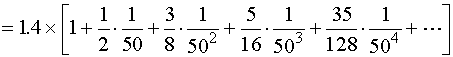
如果我们截取前四项来作计算, 则
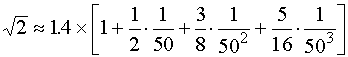
@
由于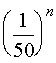 的系数
的系数 是单调递减的,其截断误差可如下估计
是单调递减的,其截断误差可如下估计

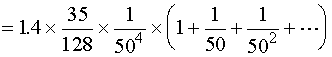

@
注明:
Ê表达式也可选其它形式,如
 ;
;
Ë在数列的极限理论学习中,我们已形究过数列
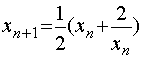 ,它单调下降,下界为
,它单调下降,下界为![]() ,且
,且![]()
利用此迭代算式,编写Matlab程序gs1101.m,运行此程序,更容易获得![]() 的高精度近似值。
的高精度近似值。
3、对数的计算
【例2】计算![]() 的近似值(精确到小数后第4位)。
的近似值(精确到小数后第4位)。
解:我们已有展开式
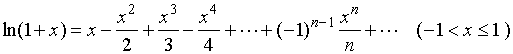
且 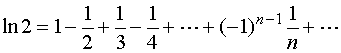
利用此数项级数来计算![]() 的近似值,理论上来说是可行的。其部分和
的近似值,理论上来说是可行的。其部分和![]() 的截断误差为
的截断误差为
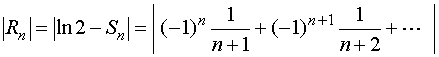
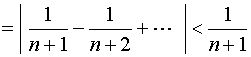
欲使精度达到![]() ,需要的项数
,需要的项数![]() 应满足
应满足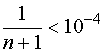 ,即
,即
![]() ,亦即,
,亦即,![]() 应要取到10000项,这实在是太大了。
应要取到10000项,这实在是太大了。
运行Matlab程序gs1102.m,取级数前一万项(n=10000)来作近似计算,可获得下表。并仔细观察项数![]() 与所求
与所求![]() 近似值对照表与计算速度。
近似值对照表与计算速度。
|
截取项数 |
ln2近似值 |
|
9900 |
0.6930971330 |
|
9991 |
0.6931972231 |
|
9992 |
0.6930971430 |
|
9993 |
0.6931972131 |
|
9994 |
0.6930971530 |
|
9995 |
0.6931972031 |
|
9996 |
0.6930971631 |
|
9997 |
0.6931971931 |
|
9998 |
0.6930971731 |
|
9999 |
0.6931971831 |
|
10000 |
0.6930971831 |
由上述程序的运行与结果,有几点感受
Ê部分和的项数取得太大,达到了一万;
Ë其近似值仅有小数点后三位是精确的;
Ì项数增加几十项,并未提供多少有效位数字;
Í计算花费了太多的时间。
这迫使我们去寻找计算ln2更有效的方法。
将展开式
![]()
中的![]() 换成
换成![]() ,得
,得
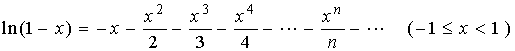
两式相减,得到不含有偶次幂的展开式
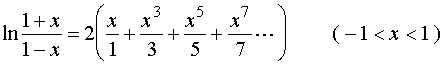
令![]() ,解出
,解出![]() 。以
。以![]() 代入得
代入得

再对此数项级数编程Matlab下的计算程序gs1103.m,运行该程序可获得项数![]() 与所求
与所求![]() 近似值对照表如下
近似值对照表如下
|
截取项数 |
ln2近似值 |
|
4 |
0.69313475733229 |
|
5 |
0.69314604739083 |
|
6 |
0.69314707375979 |
|
7 |
0.69314717025601 |
|
8 |
0.69314717954824 |
|
9 |
0.69314718045924 |
|
10 |
0.69314718054981 |
|
11 |
0.69314718055892 |
|
12 |
0.69314718055984 |
|
13 |
0.69314718055993 |
|
14 |
0.69314718055994 |
|
15 |
0.69314718055994 |
|
16 |
0.69314718055995 |
|
17 |
0.69314718055995 |
|
18 |
0.69314718055995 |
由表可发现,计算速度大大提高,近似值的精度有十分显著的改进,这种处理手段通常称作幂级数收敛的加速技术。
4、p 的计算
在小学数学学习中,我们就已接触到了圆周率p,可对它的计算却从未真正做过。现在是我们了却这一夙愿的时候了。
由展开式
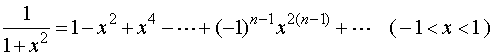
两边积分,有
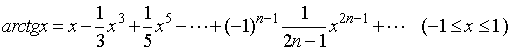
令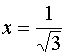 ,则
,则 ,于是有
,于是有
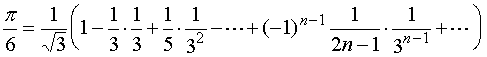
利用此式可以进行计算,效果(速度与精度)也不错,只是需要![]() 的值。借助三角公式,作适当地变形,可构造出不需要
的值。借助三角公式,作适当地变形,可构造出不需要![]() 计算表达式。
计算表达式。
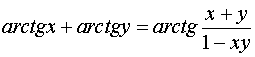
令 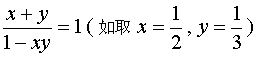 ,有
,有

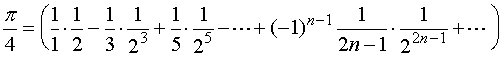

据上式,编写Matlab程序gs1104.m,运行它可获得如下结果。
|
截取项数 |
p近似值 |
|
10 |
3.141592579606 |
|
11 |
3.141592670451 |
|
12 |
3.141592649717 |
|
13 |
3.141592654485 |
|
14 |
3.141592653382 |
|
15 |
3.141592653638 |
|
16 |
3.141592653578 |
|
17 |
3.141592653592 |
|
18 |
3.141592653589 |
|
19 |
3.141592653590 |
|
20 |
3.141592653590 |
5、定积分的近似计算
【例3】计算定积分
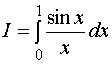
的近似值,精确到0.0001。
解:因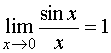 ,所给积分不是广义积分,只需定义函数在
,所给积分不是广义积分,只需定义函数在![]() 处的值为1,则它在
处的值为1,则它在![]() 上便连续了。
上便连续了。
展开被积函数,有
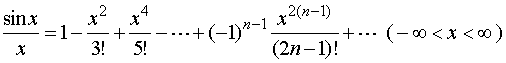
在区间![]() 上逐项积分,得
上逐项积分,得
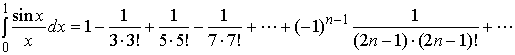
因为第四项
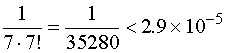
所以可取前三项的和作为积分的近似值
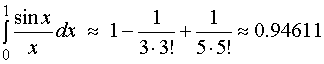
对上述级数展开式,我们编写了Matlab程序gs1105.m,运行此程序,可给出截取级数任意项时,此定积分含有更多位有效数值的近似值。
|
截取项数 |
定积分的近似值 |
|
1 |
1.00000000000000 |
|
2 |
0.94444444444444 |
|
3 |
0.94611111111111 |
|
4 |
0.94608276643991 |
|
5 |
0.94608307263235 |
|
6 |
0.94608307035488 |
|
7 |
0.94608307036723 |
|
8 |
0.94608307036718 |
|
9 |
0.94608307036718 |
|
10 |
0.94608307036718 |
二、欧拉公式
设有复数项级数为
![]() (1)
(1)
其中![]() 为实常数或实函数。如果实部所成的级数
为实常数或实函数。如果实部所成的级数
![]() (2)
(2)
收敛于和![]() ,并且虚部所成的级数
,并且虚部所成的级数
![]() (3)
(3)
收敛于和![]() ,就说级数(1)收敛且其和为
,就说级数(1)收敛且其和为![]() 。
。
如果级数(1)各项的模所构成的级数
![]() (4)
(4)
收敛,由于
![]()
则级数(2)、(3)绝对收敛,从而级数(1)收敛,这时就说级数(1)绝对收敛。
考察复数项级数
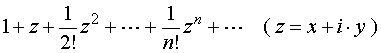 (5)
(5)
它的模所形成的级数
![]()
绝对收敛。因此,级数(5)在整个复平面上是绝对收敛的。
在![]() 轴上(
轴上(![]() ),它表示指数函数
),它表示指数函数![]() ,在整个复平面上我们用它来定义复变量指数函数,记作
,在整个复平面上我们用它来定义复变量指数函数,记作![]() 。于是定义为
。于是定义为
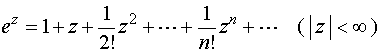 (6)
(6)
当![]() 时,
时,![]() 为纯虚数
为纯虚数![]() ,(6)式成为
,(6)式成为

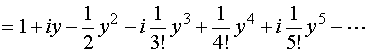

![]()
把![]() 换写为
换写为![]() ,上式变为
,上式变为
![]() (7)
(7)
这就是欧拉公式。
应用公式(7),复数![]() 可以表示为指数形式
可以表示为指数形式
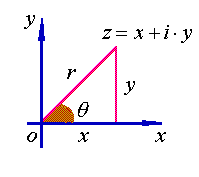
![]() (8)
(8)
其中:![]() 是
是![]() 的模,
的模,![]() 是
是![]() 的辐角。
的辐角。
在(7)式中把![]() 换为
换为![]() ,又有
,又有
![]()
与(7)相加、相减,得
 (9)
(9)
这两个式子也叫做欧拉公式。
(7)式与(9)式揭示了三角函数与复变量指数函数之间的一种联系。
根据定义(6)
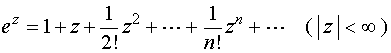
并利用幂级数的乘法,我们不难验证
![]()
特殊地,取![]() 为实数
为实数![]() ,
,![]() 为纯虚数
为纯虚数![]() ,则有
,则有
![]()
这就是说,复变量指数函数![]() 在
在![]() 处的值是模为
处的值是模为![]() 、辐角为
、辐角为![]() 的复数。
的复数。