§11.8 傅立叶级数

一、三角级数与三角函数系的正交性

描述简谐振动的函数

就是一个以为周期的正弦函数，其中ｙ表示动点的位置，ｔ表示时间，A为振幅，为角频率，为初相。

在实际问题中，还会遇到一些更复杂的周期函数，如电子技术中常用的周期为T的矩形波。

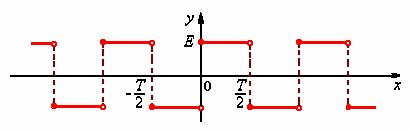
如何深入研究非正弦周期函数呢？联系到前面介绍过的用函数的幂级数展开式表示与讨论函数，我们也想将周期函数展开成由简单的周期函数例如三角函数组成的级数，具体的来说，将周期为的周期函数用一系列三角函数组成的级数来表示，记为

(1)

其中都是常数。

将周期函数按上述方式展开，它的物理意义量很明确的，这就是把一个复杂的周期运动看成是许多不同频率的简谐振动的叠加，在电工学上这种展开称为谐波分析。

为了讨论的方便，我们将正弦函数变形成为

并且令则(1)式右端的级数就可以改写为

(2)

一般地，形如(2)式的级数叫做三角级数，其中都是常数。

如同讨论幂级数时一样，我们必须讨论三角级数(2)的收敛问题，以及给定周期为2的周期函数如何把它展开成三角级数(2)。

我们首先介绍三角函数系的正交性。

所谓三角函数系

(3)

在区间[]上正交，就是指在三角函数系(3)中任何两个不同函数乘积在区间[]上的积分等于零，即

以上等式都可以通过计算定积分来验证，现将第四式验证如下。利用三角学中的积化和差公式

当时，有

在三角函数系(3)中，两个相同函数的乘积在区间[]上的积分不等于零，且有

二、函数展开成傅立叶级数

设是以为周期的周期函数，且能展开成三角级数

我们自然要问：

系数与函数之间存在怎样的关系？换句话说，如何利用把表达出来？

为此，我们进一步假设级数(4)可以逐项积分。

先求，对(4)式从－到逐项积分有

根据三角函数系(3)的正交性，等式右端除第一项外，其余各项均为零，故

于是得

其次求，用乘(4)式两端，再从－到逐项积分，我们得到

根据三角函数系(3)的正交性，等式右端除一项外，其余各项均为零，故

于是得

类似地，用乘(4)式的两端，再从－到逐项积分，可得

由于当时，的表达式正好为，因此，已得结果可以合并写成

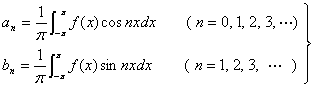(5)

如果公式(5)中的积分都存在，则系数叫做函数的傅立叶系数，将这些系数代入(4)式右端，所得的三角级数

(6)

叫做函数的傅立叶级数。

一个定义在上周期为的函数，如果它在一个周期上可积，则一定可以作出的傅立叶级数(6)，但(6)不一定收敛，即使它收敛，其和函数也不一定是，这就产生了一个问题：

需满足怎样的条件，它的傅立叶级数(6)收敛，且收敛于？换句话说，满足什么条件才能展开成傅立叶级数(6)？

下面我们叙述一个收敛定理（不加证明），它给出了关于上述问题的一个重要结论。

【定理】（收敛定理，狄利克雷充分条件）

设是周期为的周期函数，如果它满足：

1、在一个周期内连续或只有有限个第一类间断点；

2、在一个周期内至多有有限个极值点，

则的傅立叶级数收敛，并且

当是的连续点时，级数收敛于；

当是的间断点时，级数收敛于

亦即：

收敛定理告诉我们：只要函数在上至多有有限个第一类间断点，并且不作无限次振动，函数的傅立叶级数在连续点处就收敛于该点的函数值，在间断点处收敛于该点左右极限的算术平均值，可见，函数展开成傅立叶级数的条件比展开成幂级数的条件要低得多。

【例1】设是以为周期的周期函数，它在上的表达式为

将展开成傅立叶级数。

解:函数的图形如下：

函数仅在处是跳跃间断，满足收敛定理的条件，由收敛定理，的傅立叶级数收敛，并且当时，级数收敛于

当时，级数收敛于。

计算傅立叶系数如下：

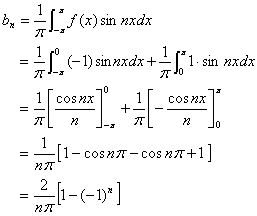
的傅立叶级数展开式为

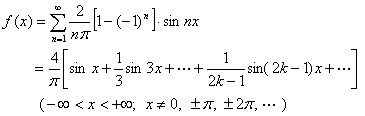
【例2】设是周期为2的周期函数，它在上的表达式为

将展开成傅立叶级数。

解：函数的图形如下：

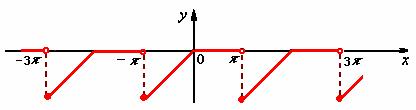
如图可知，满足收敛定理条件，在间断点处，的傅立叶级数收敛于

在连续点)处收敛于。

计算傅立叶系数如下：

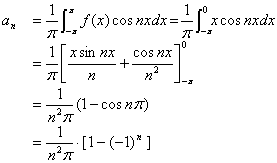
的傅立叶级数展开式为

如果函数仅仅只在[-，]上有定义，并且满足收敛定理的的条件， 仍可以展开成傅立叶级数，做法如下

1、在或外补充函数的定义，使它被拓广成周期为的周期函数，按这种方式拓广函数定义域的过程称为周期延拓。

2、将展开成傅立叶级数。

3、限制，此时，这样便得到的傅立叶级数展开式。根据收敛定理，该级数在区间端点处收敛于。

【例3】将函数 展开成傅立叶级数。

解：将在上以为周期作周期延拓，其函数图形为

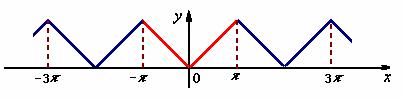
因此拓广后的周期函数在上连续，故它的傅立叶级数在上收敛于，计算傅立叶系数如下

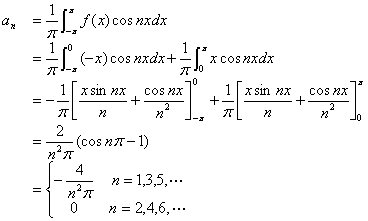
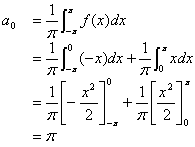
故的傅立叶级数展开式为

利用这个展开式，我们可以导出一个著名的级数和。

令，有，于是有

若记 ， ，

，

而

故

又

故