§11.9 正弦级数和余弦级数
一、奇函数偶函数的傅立叶级数
一般说来,一个函数的傅立叶级数既含有正弦项,又含有余弦项。但是,有些函数的傅立叶级数只含有正弦项或只含有余弦项,究其原因,它与所给函数的奇偶性有关。
【定理】以![]() 为周期的奇函数
为周期的奇函数![]() 展开成傅立叶级数时,它的傅立叶系数适合:
展开成傅立叶级数时,它的傅立叶系数适合:

而以![]() 为周期的偶函数
为周期的偶函数![]() 展开成傅立叶级数时,它的傅立叶系数适合:
展开成傅立叶级数时,它的傅立叶系数适合:
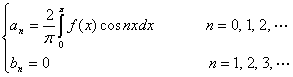
证 设![]() 是以
是以![]() 为周期的偶函数,则
为周期的偶函数,则![]() ,从而
,从而
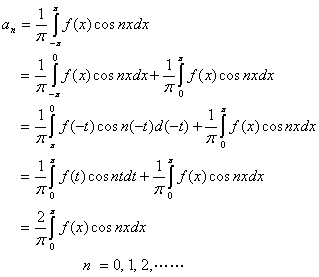
又因![]() 是
是![]() 上的奇函数,故
上的奇函数,故
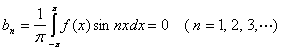
类似地可证明定理的第二部分。
该定理告诉我们:
1、如果![]() 为奇函数,那么它的傅立叶级数是只含有正弦项,不含常数项和余弦项的正弦级数
为奇函数,那么它的傅立叶级数是只含有正弦项,不含常数项和余弦项的正弦级数
![]()
2、如果![]() 为偶函数,那么它的傅立叶级数是只含有常数项和余弦项,不含正弦项的余弦级数
为偶函数,那么它的傅立叶级数是只含有常数项和余弦项,不含正弦项的余弦级数
![]()
【例1】设![]() 是周期为
是周期为![]() 的周期函数,它在
的周期函数,它在![]() 上的表达式为
上的表达式为![]() ,将它展开成傅立叶级数。
,将它展开成傅立叶级数。
解:函数的图形如下:
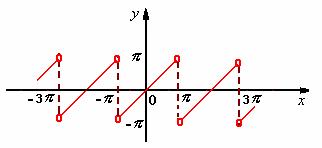
![]() 是周期为
是周期为![]() 的奇函数,因此
的奇函数,因此
![]()
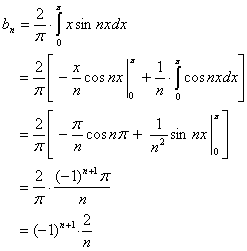
![]() 在点
在点 ![]() 不连续,据收敛定理,
不连续,据收敛定理,![]() 的傅立叶展开式为
的傅立叶展开式为
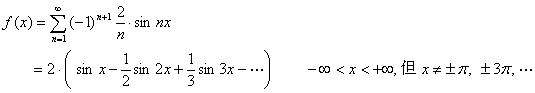
二、函数展开成正弦级数或余弦级数
如果仅给出函数![]() 在
在![]() 上的定义,如何将它展开成正弦级数或余弦级数呢?
上的定义,如何将它展开成正弦级数或余弦级数呢?
解决该问题的具体步骤如下:
1、在![]() 上重新定义新函数
上重新定义新函数![]() ,且
,且![]() 在
在![]() 上成为奇函数(或偶函数),这种定义
上成为奇函数(或偶函数),这种定义![]() 的方式称为是对
的方式称为是对![]() 的奇延拓(或偶延拓)。
的奇延拓(或偶延拓)。
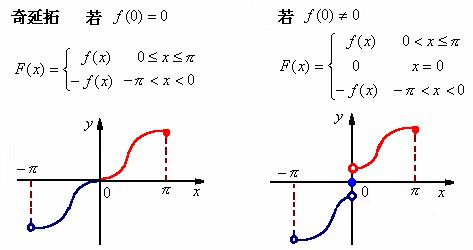
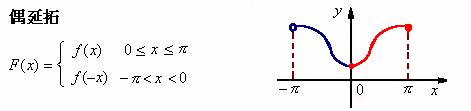
2、将![]() 以
以![]() 为周期进行周期延拓,所得函数的傅立叶展开式必为正弦级数(或余弦级数)。
为周期进行周期延拓,所得函数的傅立叶展开式必为正弦级数(或余弦级数)。
3、据![]() 的傅立叶展开式的成立区间,限制
的傅立叶展开式的成立区间,限制![]() 属于
属于![]() 、
、![]() 、
、![]() 中的某一个,此时
中的某一个,此时![]() ,这样便得到了
,这样便得到了![]() 的正弦级数(或余弦级数)。
的正弦级数(或余弦级数)。
【例2】将函数![]() 分别展开成正弦级数和余弦级数。
分别展开成正弦级数和余弦级数。
解:对![]() 进行奇延拓,得函数
进行奇延拓,得函数
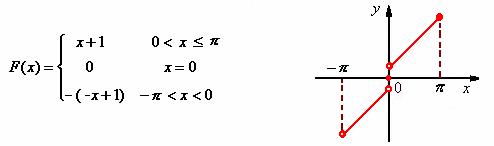
其傅立叶系数如下:
![]()
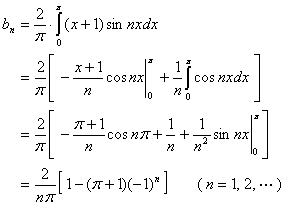
傅立叶级数为 ![]() ,据收敛定理有:
,据收敛定理有:
在![]() 处,它收敛于
处,它收敛于![]() ;
;
在![]() 处,它收敛于
处,它收敛于
![]() ;
;
在![]() 内,它收敛于
内,它收敛于![]() 。
。
故![]() 的傅立叶正弦级数展开式为
的傅立叶正弦级数展开式为
![]()
对![]() 进行偶延拓,可得函数
进行偶延拓,可得函数

其傅立叶系数为
![]()
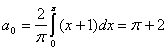

傅立叶级数为 ![]() , 据收敛定理有:
, 据收敛定理有:
在![]() 处,它收敛于
处,它收敛于
![]() ;
;
在![]() 内,它收敛于
内,它收敛于![]() 。
。
故![]() 的傅立叶余弦级数展开式为
的傅立叶余弦级数展开式为
![]()