§12.1 微分方程的基本概念

凡表示未知函数、未知函数导数与自变量之间关系的方程，称之为微分方程。微分方程中所出现的未知函数的最高阶导数的阶数，叫做微分方程的阶。

一般地，阶微分方程的形式是

Œ

其中是个变量的函数，在方程Œ式中，是必须出现的，而等变量可以出现，也可以不出现。

在以后的讨论中，我们主要讨论Œ式的特殊形式



设函数在区间上有阶导数，如果在区间上

那未函数就叫做微分方程Œ在区间上的解。

如果微分方程的解含有任意常数，且任意常数的个数与微分方程的阶数相同(这里的任意常数应相互独立，即：它们不能合并而使得任意常数的个数减少)，这样的解称之为微分方程的通解。

设微分方程为，其通解为，其中：为任意常数。为了确定任意常数的具体取值，通常给出条件

当 时，

或 Ž

这里都是给定的值。

设二阶微分方程为，其通解为，其中：为独立的任意常数。为了确定的值，通常给出条件

当 时， ， ， 即



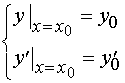
这里 都是给定的值。

上面所给出的这种条件Ž、叫做初始条件；

确定了通解中的任意常数之后所得到的解称作微分方程的特解。

求微分方程满足初始条件的特解，又称之为一阶微分方程的初值问题，记作



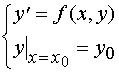
一般地讲，微分方程特解的图形是一条曲线，这一曲线称之为积分曲线。

初值问题的几何意义为：求微分方程通过点的那条积分曲线。

【例1】一曲线过点，且在该曲线上任一点处的切线斜率为，求该曲线的方程。

解：设所求曲线的方程为，则它满足

把方程两端积分，得 (是任意常数 )

由初始条件，有

由此定出

故所求曲线的方程为

【例2】验证：函数

(是任意常数)

是微分方程 的通解。

解：

，

显然

故 是微分方程的解。因是相互独立的两个任意常数，而微分方程的阶数是二阶的，故它微分方程的通解。