§12.2
可分离变量的微分方程
【定义】如果一阶微分方程能化成
![]() Œ
Œ
的形式,那么原方程称之为可分离变量的微分方程。
为讨论这类微分方程的求解,我们先看两个引例
对于一阶微分方程
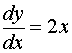
只需将上式两端积分就得到了这个方程的通解
![]()
但是,并非所有的一阶微分方程都能这样求解。
例如,对于一阶微分方程
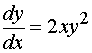
就不能直接两端取积分求出它的通解。原因是方程右端含有未知函数,积分![]() 求不出来。为了解决这个困难,在方程的两端同乘以
求不出来。为了解决这个困难,在方程的两端同乘以![]() ,使方程变为
,使方程变为 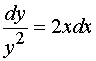
这样,变量![]() 与
与![]() 被分离在等式的两端,然后两端积分得
被分离在等式的两端,然后两端积分得
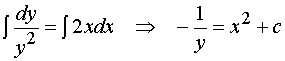
如此得到的函数是原来的微分方程的解吗?
直接验证:对方程两边关于![]() 求导,有
求导,有
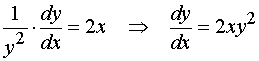
可见,它确实是原方程的通解。
下面讨论可分离变量微分方程
![]() Œ
Œ
的求解。
假定函数![]() 和
和![]() 是连续的。
是连续的。
设![]() 是方程Œ的解,将它代入方程得到恒等式
是方程Œ的解,将它代入方程得到恒等式
![]()
将上式两端积分有
![]()
引入变量替换![]() ,得
,得
![]()
设![]() 及
及![]() 依次为
依次为![]() 及
及![]() 的原函数,于是有
的原函数,于是有
![]()
因此,方程Œ的解满足关系式。
反之,如果![]() 是式所确定的隐函数,那未在
是式所确定的隐函数,那未在![]() 的条件下,据隐函数的直接求导法有
的条件下,据隐函数的直接求导法有
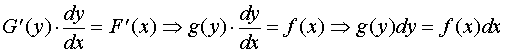
因此,函数![]() 满足方程Œ。
满足方程Œ。
综合上述讨论有
如果可分离变量方程Œ中的![]() 和
和![]() 连续,且
连续,且![]() ,那么Œ式两端积分后得到的关系式,它用隐式的形式给出了方程Œ的解。
,那么Œ式两端积分后得到的关系式,它用隐式的形式给出了方程Œ的解。
由于式含有任意常数,故式叫做微分方程的隐式通解( 当![]() 时,式所确定的隐函数也可认为是方程Œ的解)。
时,式所确定的隐函数也可认为是方程Œ的解)。
【例1】设降落伞从跳伞塔下落后,所受空气阻力与速度成正比,并设降落伞离开跳伞塔时(![]() )速度为零,求降落伞下落速度与时间的函数关系。
)速度为零,求降落伞下落速度与时间的函数关系。
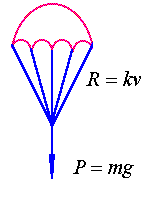
解:设伞下落速度为![]() ,在下落时,同时受到重力
,在下落时,同时受到重力![]() 与阻力
与阻力![]() 的作用,重力大小为
的作用,重力大小为![]() ,方向与
,方向与![]() 一致;阻力大小为
一致;阻力大小为![]() (
(![]() 为比例系数 ),方向与
为比例系数 ),方向与![]() 相反,从而伞所受外力为
相反,从而伞所受外力为
![]()
据牛顿第二运动定律 ![]() ,得到函数
,得到函数![]() 应满足微分方程
应满足微分方程

方程是可分离变量的,分离变量得
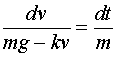
两端积分,有


其中 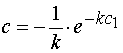
由初始条件 ![]() ,有
,有 
于是所求的函数为
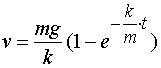
【例2】有高为100厘米的半球形容器,水从它的底部小孔流出,小孔横截面面积为1平方厘米,开始时容器内盛满了水,求水从小孔流出过程中容器里的水面的高度![]() ( 水面与孔口中心间的距离 )随时间
( 水面与孔口中心间的距离 )随时间![]() 变化的规律。
变化的规律。
解:由水力学知道,水从孔口流出的流量![]() ( 即通过孔口横截面的水的体积
( 即通过孔口横截面的水的体积![]() 对时间
对时间![]() 的变化率 )可用下列公式计算
的变化率 )可用下列公式计算

这里,![]() 为流量系数,
为流量系数,![]() 为孔口横截面面积,
为孔口横截面面积,![]() 为重力加速度。
为重力加速度。
现在,孔口横截面面积为![]()

另一方面,设在微小时间间隔![]() 内,水面高度由
内,水面高度由![]() 降至
降至![]() ,可得到
,可得到 ![]()
其中![]() 是时刻
是时刻![]() 时的水面半径,右端置负号是由于
时的水面半径,右端置负号是由于![]() ,而
,而![]() 。
。
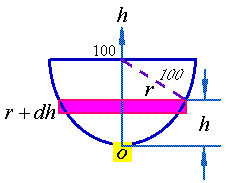
如图,![]()
![]()
得到微分方程 ![]()
及初始条件 ![]()
方程是可分离变量的方程
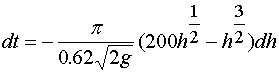

将初始条件代入,定出常数![]() 。
。


把![]() 值代入并化简,得
值代入并化简,得
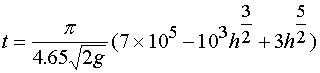
【注记】
本例通过对微小量的分析,得到了微分方程。这种微小量分析法,是建立微分方程的一种常用方法。