§12.3 齐次方程

如果一阶微分方程

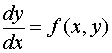
中的可写成的函数，即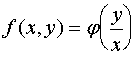，称此方程为齐次方程。

例如 是齐次方程，因为

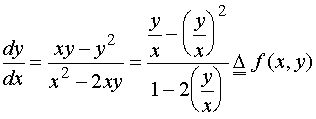
在齐次方程

中，引入变量替换

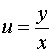
有 ，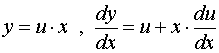

将它们代入齐次方程，得

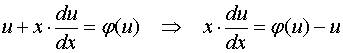
分离变量，得

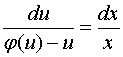
两边积分，得

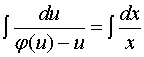
求出积分后，再用代替，便得所给齐次方程的隐式通解。

【例1】解方程

解： 原方程可写成

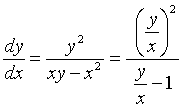
因此是齐次方程，令 ，则

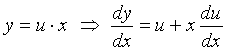
于是原方程变为

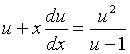
分离变量， 得

两边积分，得

以代替， 得到原方程的通解

注记:

齐次方程的求解实际上是通过变量替换，将方程化为可分离变量的方程。

变量替换法在解微分方程中，有着特殊的作用。但困难之处是如何选择适宜的变量替换。一般来说，变量替换的选择并无一定之规，往往要根据所考虑的微分方程的特点而构造。对于初学者，不妨多试一试，尝试几个直接了当的变量替换。

【例2】求下列微分方程的通解

1、

2、

解1、令,则

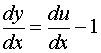
原方程化为

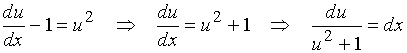
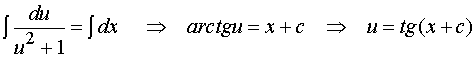
即

解2、

令 ，原方程可化为

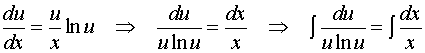
(其中 )

【例3】设河边点的正对岸为点，河宽，两岸为平行直线，水流速度为。有鸭子从点游向点，设鸭子(在静水中)的游速为，且鸭子游动方向始终朝着点，求鸭子游过的迹线。

解：设水流速度为，鸭子游速为，则鸭子实际运动速度为。

取为坐标原点，河岸朝顺水方向为轴，轴指向对岸，设在时刻鸭子位于点。

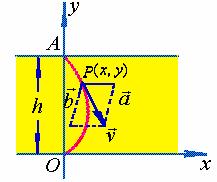
设鸭子运动速度为

，

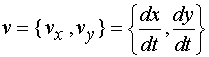故有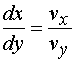

而 ，

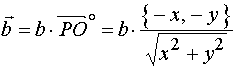
从而

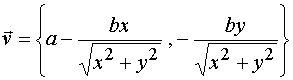
由此得到微分方程

即

令 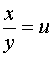，则 ，，代入上面的方程有

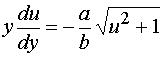
分离变量得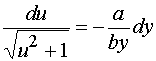

积分得

，

，

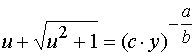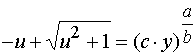
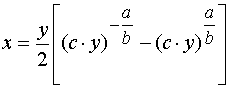
以条件时代入上式，得 ，故鸭子游过的迹线为