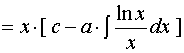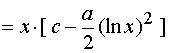§12.4 一阶线性非齐次微分方程

一、线性方程

方程

Œ

叫做一阶线性微分方程(因为它对于未知函数及其导数均为一次的)。

如果 ，则方程称为齐次的；

如果 不恒等于零，则方程称为非齐次的。

首先，我们讨论Œ式所对应的齐次方程



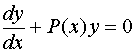
的通解问题。

分离变量得

两边积分得

或

其次，我们使用所谓的常数变易法来求非齐次线性方程Œ的通解。

将Œ的通解中的常数换成的未知函数，即作变换

两边乘以得

两边求导得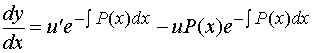

代入方程Œ得

，

于是得到非齐次线性方程Œ的通解

将它写成两项之和

不难发现：

第一项是对应的齐次线性方程的通解；

第二项是非齐次线性方程Œ的一个特解。

由此得到一阶线性非齐次方程的通解之结构。

【例1】求方程

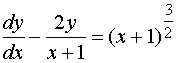
的通解。

解：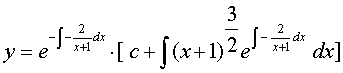

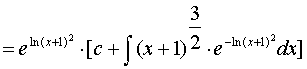
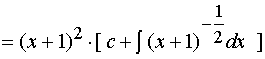
由此例的求解可知，若能确定一个方程为一阶线性非齐次方程，求解它只需套用公式。

二、贝努利方程

方程

叫做贝努利方程。

当时，它是一阶线性非齐次微分方程

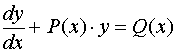
当时，它是一阶线性齐次微分方程

当时，它是一阶非线性的微分方程，通过变量代换可化归为一阶线性微分方程。

具体解法如下：

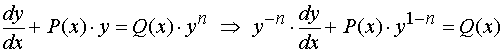
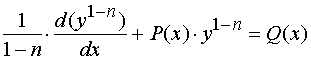
令 ，方程化为关于的一阶线性非齐次微分方程

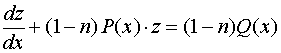
【例2】求贝努利 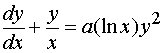的通解。

解 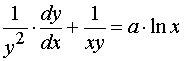： ，
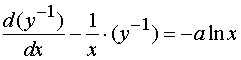
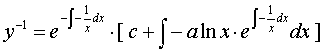