§12.5 全微分方程

一、定义

一阶微分方程写成

Œ

形式后，如果它的左端恰好是某一函数的全微分，即

则方程Œ就叫做全微分方程。

二、全微分方程的求解

设方程Œ是一个全微分方程，则存在二元函数，使得

则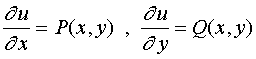

方程Œ可写成 

如果是Œ的解，那么这个解也满足方程，故

因此

这表明，Œ的解是由方程所确定的隐函数。

反过来，若方程确定了一个可微分的隐函数，

则

两端对求导得

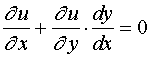
或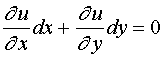

即

这表明，由方程所确定的隐函数是方程Œ的解。

综合上述两点， 我们有结论

全微分方程Œ的解是由所确定的隐函数，而由所确定的隐函数一定是方程Œ的解。

因此，若方程Œ的左端是函数的全微分，那么它的通解为

其中是任意常数。

三、方程Œ是全微分方程的条件

若，在单连通域内具有一阶连续偏导数，则方程Œ成为全微分方程的充要条件为

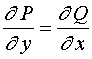Ž

在内恒成立。

四、全微分函数的求法

当条件Ž满足时，全微分函数可以通过对坐标的曲线积分获得

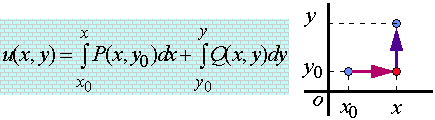
或

【例1】求解

解：这里

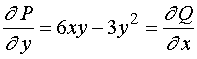
所以这是全微分方程，有

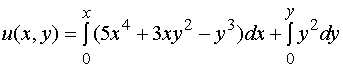
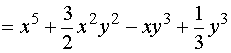
于是，方程的通解为

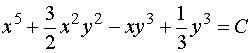
五、积分因子

当条件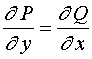不能满足时，方程Œ

就不是全微分方程。

如果找得到一个函数，使方程

成为全微分方程，则称函数称为方程Œ的积分因子。

例如方程 ，有

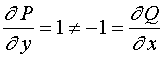
故该方程不是全微分方程。

但方程两端乘上因子以后，方程

变成为全微分方程。事实上

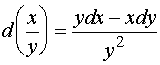
因此，是上述方程的一个积分因子。

一般说来，积分因子的确定并不简单，而且积分因子往往不唯一的。不难验证和也是上述方程的积分因子。

如果对函数的微分运算十分熟练，往往可以通过观察得到积分因子。

【例2】用观察法求下列方程的积分因子， 并求其通解

1、

2、

解1：是一个积分因子，乘上该因子之后，方程成为

，

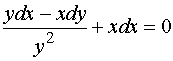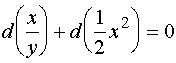
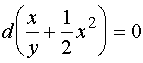
故通解为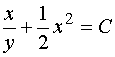

解2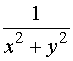：是一个积分因子

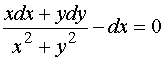
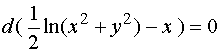
故通解为