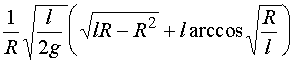§12.7
可降阶的高阶微分方程
前面，我们主要讨论了一阶微分方程的求解问题，对于二阶及二阶以上的微分方程(即高阶微分方程)，原则上讲，可以通过适当的变量替换化成低阶的方程来求解。自然地，选择适合的变量替换往往是一件困难的事情。
下面，我们仅究三类较简单的高阶方程的求解展开讨论。
一、
型的微分方程
微分方程
的右端仅含有自变量
，只要把
作为新的未知函数，那么就是新未知函数的一阶微分方程，两边积分，就得到一个 
阶的微分方程
同理 
依此类推，连续积分
次，便得到了方程的含有个任意常数的通解。
【例1】求
的通解。
解：
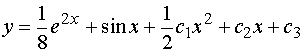
其中
是任意常数。
二、
型的微分方程
微分方程
的右端不显含有未知函数
。
如果作变量替换
，则 
方程可化为
这是一个关于变量
的一阶微分方程，设其通解为
由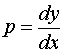
，又得以一个一阶微分方程
因此，方程的通解为
其中
是任意常数。
【例2】求微分方程
满足初始条件
的特解。
解：设
，将之代入方程，得
分离变量有
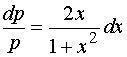
两边积分，得
由条件
，得
从而 
再积分，得 
又由条件
，得 
故所求特解为 
注记：
求高阶方程满足初始条件的特解时，对任意常数应尽可能及时定出来，而不要待求出通解之后再逐一确定，这样处理会使运算大大简化。
三、
型微分方程
微分方程
的右端不显含自变量。
作变量替换，利用复合函数求导法则，可将
写成如下形式
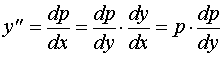
方程可化成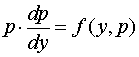 
这是一个关于变量
的一阶微分方程，设求出它的通解为
从而有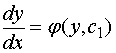 
分离变量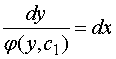 
，
再积分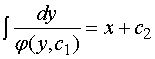 
，便可得到方程的通解。
【例3】求
的通解。
解：设 ，则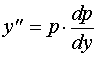 
分离变量，得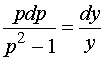 
两边积分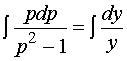 
有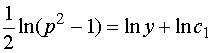 
，
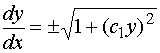
分离变量，再积分，得
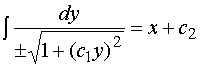
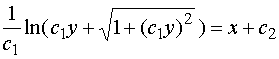
其中
是任意常数。
【例4】一个离地面很高的物体，受地球引力的作用由静止开始落向地面，求它落到地面时的速度和所需时间( 不计空气阻力 )。
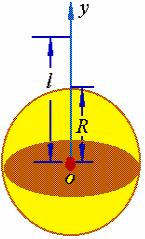
解：取连结地球中心与该物体的直线为轴，其方向铅直向上，取地球中心在原点
。设物体的质量为
，物体下落时与地球中心的距离为
，地球半径为
，在时刻
物体所在位置为
。
于是，速度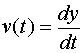
，据万有引力定律，有以下微分方程
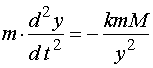
其中：为地球质量，
为引力常数，因
，且当
时，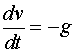
(这里置负号是由于物体运动加速度的方向与轴的正向相反)，故
， 
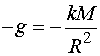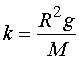
于是方程可写成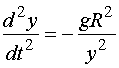 
初始条件是 
， 
先求物体到达地面的速度，由 
，则
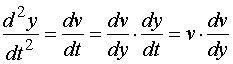
代入原方程，得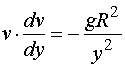 
分离变量，得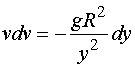 
再求积分，得 
将初始条件
，代入得
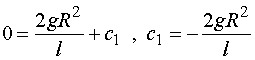
于是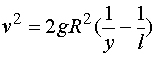 
在式中令， 得到物体到达地面时的速度
为
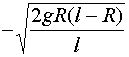
这里取负号是由于物体运动方向与轴的正向相反。
下面再求物体落到地面所需时间
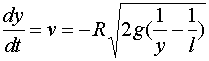
分离变量，得
两端积分，得
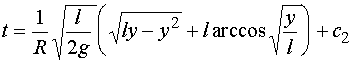
由条件 
，得 
于是上式成为
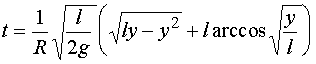
在上式中令，便得到物体到达地面所需的时间为
