§12.8 高阶线性微分方程

一、二阶线性微分方程的引入

【例1】设有一弹簧，它的上端固定，下端挂一个质量为的物体。当物体处于静止状态时，作用在物体上的重力与弹性力大小相等，方向相反。这个位置就是物体的平衡位置。如图，取轴铅直向下，并取物体的平衡位置为坐标原点。

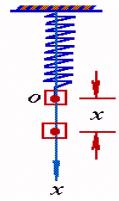
如果使物体具有一个初始速度，那未物体便离开平衡位置，并在平衡位置附近作上下振动。在振动过程中，物体的位置随时间变化，即是的函数

试确定物体的振动规律。

力学知识告诉我们：弹簧使物体回到平衡位置的弹性恢复力和物体离开平衡位置的位移成正比，即

其中为弹簧的弹性系数，负号表示弹性恢复力方向和物体位移方向相反。

另外，物体在运动过程中还受到阻尼介质(如空气、油等)的阻力作用，使得振动逐渐趋向于停止。由实验知道，阻力总与运动方向相反，当振动不大时，其大小与物体运动的速度成正比，设比例系数为，则有

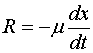
根据上述关于物体受力情况的分析， 由牛顿第二定律得

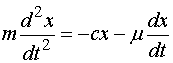
移项，并记 ，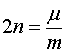

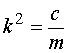
则上式化为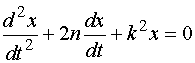

这就是在有阻尼的情况下，物体自由振动的微分方程。

如果物体在振动过程中， 还受到铅直干扰力

的作用，则有

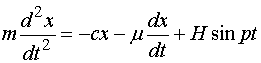
即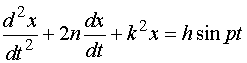

其中，这就是强迫振动的微分方程。

观察上述微分方程的特点，它可表示成一个更一般的形式

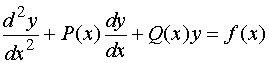Œ

方程Œ叫做二阶线性微分方程。当方程的右端时，方程叫做齐次的;否则，方程叫做非齐次的。

二、二阶齐次线性微分方程的通解结构

【定理一】如果函数与是二阶齐次线性方程



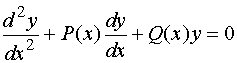
的两个解，则

Ž

也是方程的解，其中，是任意常数。

证明：将表达式Ž代入式，有

故Ž式是方程的解。

这一性质表明，齐次线性方程的解符合叠加原理。

值得注意的是，叠加起来的解Ž从形式上看含有两个任意常数， 但它不一定是方程的通解。

例如，设是的一个解，则也是的解，这时Ž式成为

可以把它写成

( 其中 )

这显然不是的通解。

这样便提出了一个问题，在什么情况下，Ž式才是方程的通解呢?

要解决这一问题，我们还需引入一个新的概念，即所谓函数的线性相关与线性无关。

设为定义在区间内的个函数，如果存在个不全为零的常数，使得当在该区间内有恒等式

成立，那未称这个函数在区间内线性相关；否则称线性无关。

例如，函数在整个数轴上是线性相关的。

因为取，就有恒等式

又例如，函数在整个数轴上是线性无关的。

因为对于不全为零的数 ，一元二次方程

至多只有两个实根。因此，它不会恒等于零。

下面，我们寻找两个函数线性相关的条件

给定两个函数，若它们线性相关，则

存在两个不全为零的常数( 不妨认为 )， 使得

( 常数 )

反过来，如果 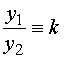( 常数 )

则

即是线性相关的。

因此，我们得到结论：

函数与线性相关的充要条件是恒等于常数。

由于函数的线性相关与线性无关是互逆的概念， 因此， 函数与线性无关的充要条件是不恒等于常数。

现在，我们给出二阶线性齐次微分方程的通解结构定理。

【定理二】如果与是方程

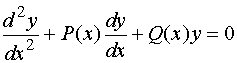
的两个线性无关的特解，则

(其中 为任意常数)

就是方程的通解。

【例1】验证：函数与是二阶线性齐次方程

的两个解，求该方程的通解。

解：

故 与 均为方程的解。

又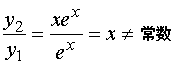

故 是方程的通解。

三、二阶线性非齐次微分方程的通解结构

【定理三】设是二阶线性齐次方程

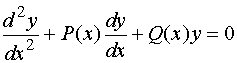
的通解，而是二阶线性非齐次线性方程

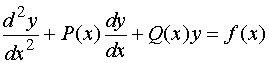
的一个特解，那未

是二阶线性非齐次微分方程的通解。

证明：将代入非齐次方程， 有

故 是方程的解，由于齐次的通解含有两个独立的任意常数，故它是非齐次方程的通解。

求非齐次方程的特解时，下述定理会经常用到。

【定理四】设与分别是二阶线性非齐次微分方程

与

的特解，则是二阶线性非齐次微分方程

的特解。

这一定理的证明较简单，只需将代入方程

便可验证。

这一结论告诉我们

欲求方程 特解

可分别求

与

的特解和，然后进行叠加

最后指出，在本节，我们仅讨论了二阶线性齐次(非齐次)微分方程的通解之结构，并未给出求解二阶线性微分方程的方法。