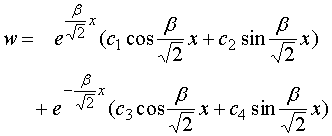§12.9
二阶常系数齐次线性微分方程
一、二阶常系数齐次线性微分方程的一般形式
方程
![]() Œ
Œ
其中![]() 是常数,称之为二阶常系数齐次线性方程;
是常数,称之为二阶常系数齐次线性方程;
如果![]() 不全为常数, 则称它为二阶变系数齐次线性微分方程。
不全为常数, 则称它为二阶变系数齐次线性微分方程。
二、二阶常系数齐次线性微分方程的通解
由第八节的讨论可知,要找微分方程Œ的通解,可先求出它的两个解![]() 与
与![]() ,如果
,如果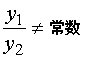 ,即
,即![]() 与
与![]() 线性无关,那未
线性无关,那未 ![]() 就是方程的通解。
就是方程的通解。
对于指数函数![]() ,若它是方程Œ的解,则有
,若它是方程Œ的解,则有
![]()
![]()
![]()
![]()
由于![]() ,从而有
,从而有
![]()
由此可见,只要![]() 满足代数方程,函数
满足代数方程,函数![]() 就是微分方程Œ的解。我们把此代数方程叫做微分方程Œ的特征方程。
就是微分方程Œ的解。我们把此代数方程叫做微分方程Œ的特征方程。

特征方程的两个根![]() ,可用公式
,可用公式
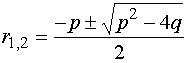
求出,它们有三种不同的情形:
(1)、当![]() 时,
时,![]() 是两个不相等的实根:
是两个不相等的实根:
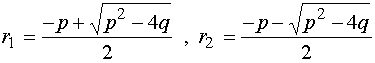
(2)、当![]() 时,
时,![]() 是两个相等的实根:
是两个相等的实根:
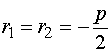
(3)、当![]() 时,
时,![]() 是一对共轭复根:
是一对共轭复根:
![]()
其中 
相应地,微分方程Œ的通解也就有三种不同的情形,现分别讨论如下:
(1)、特征方程有两个不相等的实根:![]()
由上面的讨论知道,![]() 与
与![]() 均是微分方程的两个解,并且
均是微分方程的两个解,并且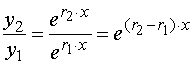 不是常数,因此微分方程Œ的通解为
不是常数,因此微分方程Œ的通解为
![]()
(2)、特征方程有两个相等的实根:![]()
这时,我们只得到微分方程Œ的一个解
![]() ,为了得到方程的通解,我们还需另求一个解
,为了得到方程的通解,我们还需另求一个解![]() ,并且要求
,并且要求 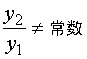 。
。
设 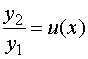 ,即
,即 ![]() ,下面来求
,下面来求![]() 。
。
![]()
![]()
![]()
![]()
![]()
相加,得 ![]()
约去![]() ,整理得
,整理得
![]()
由于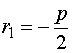 是特征方程的二重根,因此
是特征方程的二重根,因此
![]()
于是, ![]()
因只要得到一个不为常数的解,可取![]() ,由此得到微分方程的另一个解
,由此得到微分方程的另一个解
![]()
从而得到微分方程Œ的通解为
![]()
(3)、特征方程有一对共轭复根:![]()
![]()
![]()
是微分方程Œ的两个解,根据齐次方程解的叠加原理,
有
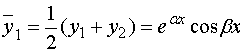

也是微分方程Œ的解,且
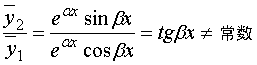
所以,微分方程Œ的通解为
![]()
综上所述,求二阶常系数齐次线性微分方程
![]() Œ
Œ
的通解的步骤如下
第一步 写出微分方程Œ的特征方程
![]()
第二步 求出特征方程的两个根![]() 。
。
第三步 据特征方程的两个根的不同情形, 依下表写出微分方程的通解。
|
特征方程 |
微分方程 |
|
两个不相等的实根 |
|
|
两个相等的实根 |
|
|
一对共轭复根 |
|
【例1】求微分方程 ![]() 的通解。
的通解。
解:所给微分方程的特征方程为
![]()
其根为 ![]()
因此所求通解为 ![]()
【例2】求微分方程![]() 的通解。
的通解。
解:所给方程的特征方程为
![]()
其根为 
因此所求通解为 ![]()
三、![]() 阶常系数齐次线性微分方程
阶常系数齐次线性微分方程
![]() 阶常系数齐次线性微分方程的一般形式是
阶常系数齐次线性微分方程的一般形式是
![]() Ž
Ž
其中![]() 都是常数。
都是常数。
令 ![]()
那未 ![]()
将![]() 代入方程, 得
代入方程, 得
![]()
可见,如果选取![]() 是
是![]() 次代数方程
次代数方程
![]()
的根,那么函数![]() 就是方程Ž的一个解。
就是方程Ž的一个解。
方程叫做微分方程Ž的特征方程。
根据特征方程的根,可以写出其对应的微分方程的解如下
|
特 征 方 程 的 根
|
微 分 方 程 通 解 中 对 应 的 项 |
|
(1) 单实根 |
给出一项:
|
|
(2) 一对单复根 |
给出两项:
|
|
(3) |
给出 |
|
(4) 一对
|
给出
|
从代数学知道,![]() 次特征方程有
次特征方程有![]() 个根,且每一个根都对应着通解中的一项,而每项中又各含一个任意常数,这样就得到了
个根,且每一个根都对应着通解中的一项,而每项中又各含一个任意常数,这样就得到了![]() 阶常系数齐次线性微分方程的通解。
阶常系数齐次线性微分方程的通解。
【例3】求微分方程![]() 的通解。
的通解。
解:特征方程 ![]()
![]()
其特征根为 ![]() (二重),
(二重),![]()
故微分方程的通解为
![]()
【例4】求微分方程
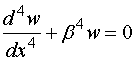 的通解。
的通解。
解:特征方程为 ![]()
![]()
![]()
![]()
特征根为  ,
,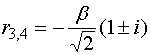
故方程的通解为