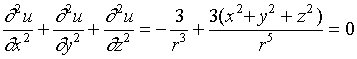§8.2 偏导数

一、偏导数定义、计算法及几何意义

1、定义

由于多元函数的自变量不止一个，因变量与自变量的关系要比一元函数复杂得多。本节，我们以二元函数为例，考虑二元函数关于其中一个自变量的变化率的问题。

若只有自变量变化，而自变量固定(即看作常量)，这时，就成了一元函数，这个函数对于的导数，就称之为二元函数对于的偏导数。

【定义】设函数在点的某一邻域内有定义，当固定在，而在处有增量时，相应地函数有增量

如果极限

存在，则称此极限为函数在点处对的偏导数，并记作

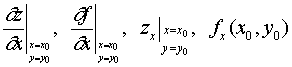
即 (1)

类似地，函数在点处对的偏导数定义为

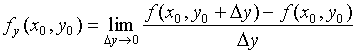
如果函数在区域内每一点处对的偏导数都存在，那未这个偏导数就是的函数，称它为函数对自变量的偏导函数，记作 。

类似地，可以定义函数对自变量的偏导函数，并记作

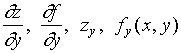
由偏导函数概念可知，在点处对的偏导数，其实就是偏导函数在点处的函数值；就是偏导函数在点处的函数值。

在不产生混淆的情况下，我们以后把偏导函数也简称为偏导数。

2、计算法

求的偏导数，并不需要新的方法，因为这里只有一个自变量在变化，另一自变量被看成是固定的，所以仍然是一元函数的导数。

求时，把看作常量，而对求导数；

求时，把看作常量，而对求导数。

显然，偏导数的概念可推广到三元以上的函数情形。

例如，三元函数在点处对的偏导数是如下极限

【例1】求在点处的偏导数。

【解法一】 ,

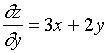
则 ,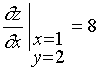

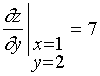
【解法二】 ，

则

注：求多元函数在某点处的偏导数时，解法二有时会方便一些。

【例2】设 ( , ,为任意实数 )

求证：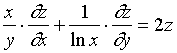

证明：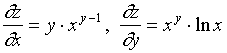

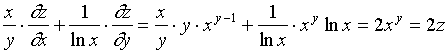
【例3】已知理想气体的状态方程为( 为常量 )，

求证：

证明：

故

注:偏导数的记号应看作一个整体性的符号(不能看成商的形式)，这与一元函数导数可看作函数微分与自变量微分之商是有区别的。

3、几何意义

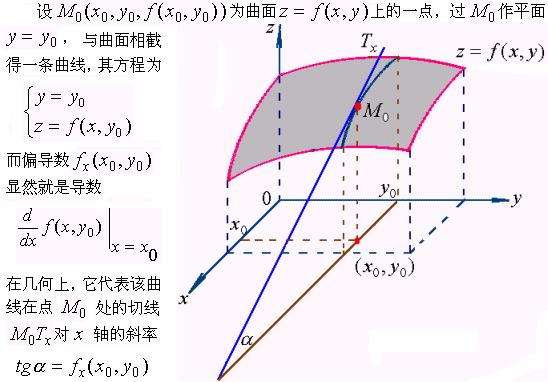
同样，偏导数表示曲面被平面所截得的曲线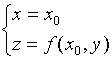在点处的切线对轴的斜率。

4、二元函数的偏导数与连续性之间的关系

一元函数在某点可导，则函数在该点一定连续；若函数在某点不连续，则函数在该点一定不可导。对于二元函数来说，情况就不同了。

二元函数在点处的偏导数、，仅仅是函数沿两个特殊方向( 平行于轴、轴 )的变化率；而函数在点连续，则要求点沿任何方式趋近于点时，函数值趋近于，它反映的是函数在点处的一种“全面”的性态。

因此，二元函数在某点偏导数与函数在该点的连续性之间没有联系。

【反例一】讨论函数

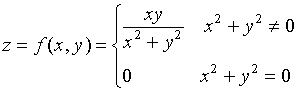
在点处的偏导数与连续性。

解：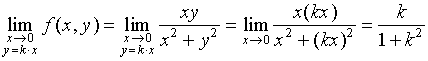

函数沿过原点的直线趋近于原点时，其极限值与参数有关，故二重极限不存在，函数在原点自然是不连续的。

函数关于自变量是对称的，故

此例表明，二元函数在一点不连续，但其偏导数却存在。

【反例二】讨论函数

在点处的偏导数与连续性。

解：显然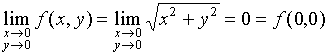，,函数在原点连续。

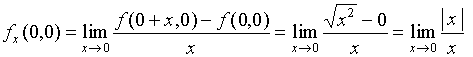不存在，

据对称性，也不存在。

此例表明，二元函数在一点连续，但在该点的偏导数不存在。

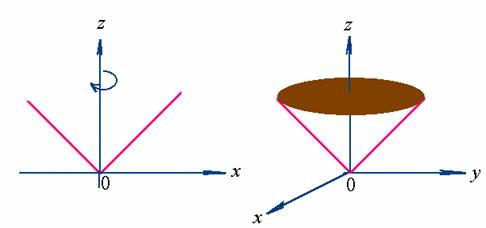
在几何上，曲面可看成是折线绕轴旋转而成的锥面，点是曲面的尖点。

二、高阶偏导数

设函数在区域内具有偏导数

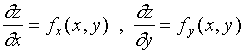
于是，在内、均是的函数，若这两个函数的偏导数也存在，则称它们是函数的二阶偏导数。

按照对变量求导次序有下列四种二阶偏导数

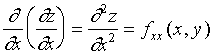
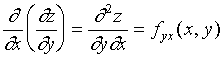
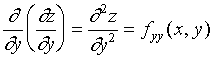
其中：称、为二阶混合偏导数，类似地，可得到三阶、四阶和更高阶的导数。二阶及二阶以上的偏导数统称为高阶偏导数。

对于二阶偏导数的符号，有必要引入如下简洁记法：

，

，

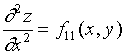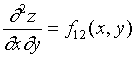
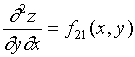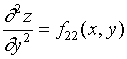
在不特别需要写出函数自变量时，二阶偏导数的符号还可简单的记成

【例4】求函数的二阶偏导数。

解：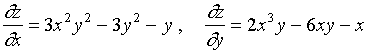

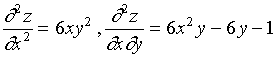
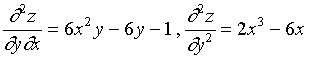
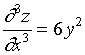
此例中的两个二阶混合偏导数相等，即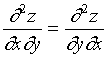，这并不是某种偶然的巧合，其实，我们有如下定理。

【定理】如果函数的两个二阶混合偏导数及在区域内连续，那未在该区域内这两个二阶混合偏导数必相等。

这一结论表明，有二阶混合偏导数连续的条件下，它与求导次序无关。

对于二元以上的函数，我们可类似地定义高阶偏导数，而且高阶混合偏导数在偏导数连续的条件下也与求导的次序无关。

必须指出，定理中所要求的条件连续是必要的，改变这一条件，定理的结论不真。

【例5】证明函数

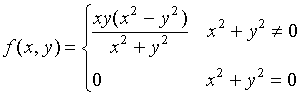
在原点处的两个二阶混合偏导数存在，但不相等。

证明：当时，

当时，

即

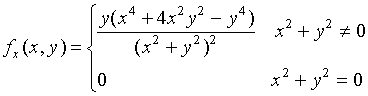
从而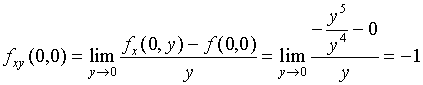

注意到，将函数中的变量与对调，函数却改变符号，于是有

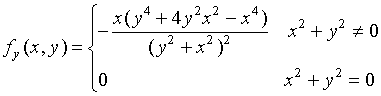
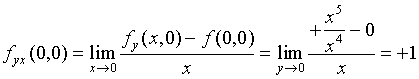
这里 , 显然，两个一阶偏导函数在原点是不连续的。

【例6】证明函数 (这里 )满足拉普拉斯方程

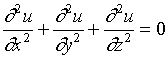
证明

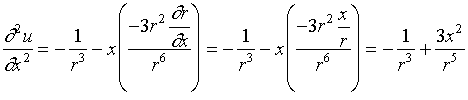
由于函数关于自变量是对称的，因此

,

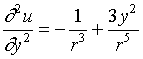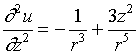
故