§8.3 全微分

一、全微分的定义

给定二元函数，且 均存在，由一元微分学中函数增量与微分的关系，有

上述二式的左端分别称之为二元函数对或的偏增量，而右端称之为二元函数对或的偏微分。

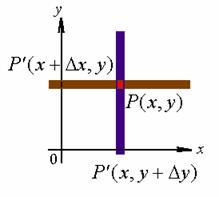
为了研究多元函数中各个自变量都取得增量时，因变量所获得的增量，即全增量的问题，我们先给出函数的全增量的概念。

【定义】 设二元函数在点的某邻域内有定义，点为该邻域内的任意一点，则称这两点的函数值之差

为函数在点处对应于自变量增量与的全增量，记作。

即 (1)

一般说来，全增量的计算往往较复杂，参照一元函数微分的做法，我们希望用自变量增量与的线性函数来近似地代替，特引入下述定义。

【定义】如果函数在点的全增量

可表示成为

(2)

其中，,为不依赖于与，而仅与有关，

则称函数在点处可微分。

而称为函数在点处的全微分，记作

二、函数可微分的条件

【定理一】（必要条件）

如果函数在点处可微分，则函数在点处的偏导数, 必定存在，且函数在点的全微分为

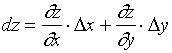(3)

证明：设函数在点可微分。于是，对点某一邻域内的任意一点，(2)式总成立。

特别地，当时，(2)式也成立，这时，即

于是

从而，偏导数存在且等于。

同理可证

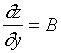
故(3)式成立。

【定理二】（充分条件）

如果函数的偏导数和在点连续，则函数在该点可微分。

证明：因在点的偏导数,连续，故在点的某一邻域内,存在。

设为该邻域内任意一点，则

应用拉格朗日中值定理有

又在点连续，于是

，其中。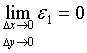

于是

同理可证

，其中 .

于是，全增量可表示成为

而

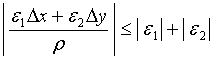
当，即时，它是趋近于零的。

因此

故函数 在点 可微分。

三、几个关系

(1)、若函数在点处可微分，则函数在该点连续。

事实上，

则 。

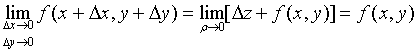
注意到 等价。

(2)、函数的偏导数, 存在只是函数全微分存在的必要条件，而不是充分条件。

【反例一】函数

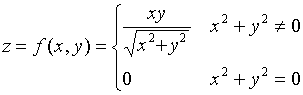
在点处有

类似地

从而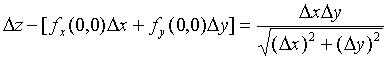

考虑点沿直线趋近于，则

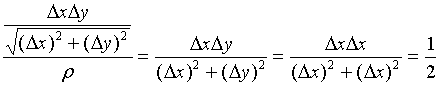
它不能随而趋近于，即当时，

并不是一个较高阶的无穷小，因此，函数在点的全微分不存在。

(3)、若函数在点可微分，则偏导数,在该点存在但不一定连续。

【反例二】函数

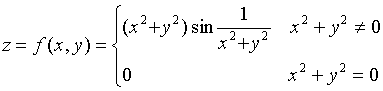
在点可微分，但偏导数在点处不连续。

证明：

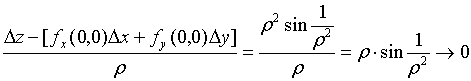
( 当 时 )

故函数在处的微分存在,且 。

而

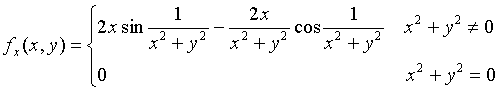
当点沿直线趋向于时,极限

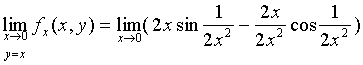
不存在。故 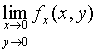不存在,在点处不连续。

综合上述讨论，我们有结论

最后，我们指出：上述概念、定理及结论均要相应地推广到二元以上的函数。习惯上，我们用记，记，并称为自变量,的微分，这样函数的全微分可写成

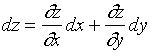(4)

通常，我们把二元函数的全微分等于它的两个偏微分之和，即(4)式称之为二元函数微分的叠加原理。

叠加原理也适用于二元以上函数的情形,如果三元函数可微分,那么

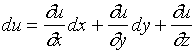
【例1】求函数 的全微分。

解: 因 , ,

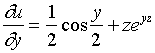则

【例2】计算函数 在点 处的全微分。

解: ,

,

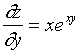
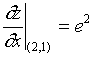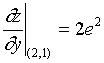
故