§8.4
多元函数求导法则
【定理】若函数![]() 及
及![]() 都在点
都在点![]() 可导;
可导;
函数![]() 在对应点
在对应点![]() 具有连续偏导数,
具有连续偏导数,
则复合函数![]() 在点
在点![]() 可导,且其导数为
可导,且其导数为
![]() (1)
(1)
证明:设![]() 获得增量
获得增量![]() ,这时
,这时![]() 的对应增量为
的对应增量为![]() ,函数
,函数![]() 的对应增量为
的对应增量为![]() 。
。
据假定,函数![]() 在点
在点![]() 具有连续偏导数,从而有
具有连续偏导数,从而有
![]()
这里,当![]() 时,
时,![]() 。
。
上式两边除以![]() 得
得
![]()
而当![]() 时,有
时,有 ![]() ,从而
,从而
![]()
所以
![]()
故复合函数
![]() 在点
在点![]() 可导,其导数可用(1)式计算。
可导,其导数可用(1)式计算。
用同样的方法,可把定理推广到复合函数的中间变量多于两个的情形。
例如, 设 ![]() 与
与 ![]() 复合而得到
复合而得到
函数 ![]() 。
。
若![]() 在点
在点![]() 可导,
可导,
![]() 对
对![]() 具有连续偏导数,
具有连续偏导数,
则复合函数![]() 在点
在点![]() 可导, 且
可导, 且
![]() (2)
(2)
在公式(1)与(2)中的导数称为全导数。
上述定理还可推广到中间变量不是一元函数而是多元函数的情形。
例如, 设![]() 与
与 ![]() 复合而得到
复合而得到
函数 ![]() ,
,
若 ![]() 在点
在点 ![]() 具有对
具有对![]() 及
及![]() 的偏导数,
的偏导数,
函数![]() 在对应点
在对应点![]() 具有连续偏导数,
具有连续偏导数,
则![]() 在点
在点![]() 的两个偏导数存在, 且
的两个偏导数存在, 且
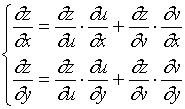 (3)
(3)
事实上,求![]() 时,
时,![]() 看作常量,因此中间变量
看作常量,因此中间变量![]() 及
及![]() 仍可看作一元函数而应用上述定理。但
仍可看作一元函数而应用上述定理。但![]() 均是
均是![]() 的二元函数,所以应把(1)式中的
的二元函数,所以应把(1)式中的![]() 直导数记号改为
直导数记号改为![]() 偏导数的记号,再将
偏导数的记号,再将![]() 换成
换成![]() ,这样便得到了(3)式。
,这样便得到了(3)式。
类似地, 设![]() 及
及![]() 均在点
均在点![]() 具有对
具有对![]() 及
及![]() 的偏导数,而函数
的偏导数,而函数![]() 在对应点
在对应点![]() 具有连续偏导数,则复合函数
具有连续偏导数,则复合函数
![]()
在点![]() 的两个偏导数都存在,且
的两个偏导数都存在,且
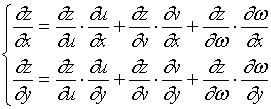 (4)
(4)
例如,若![]() 有连续偏导数,而
有连续偏导数,而![]() 偏导数存在,则复合函数
偏导数存在,则复合函数 ![]() 可看作上述情形中当
可看作上述情形中当![]() 的特殊情形, 因此
的特殊情形, 因此
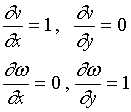
(4)式变成
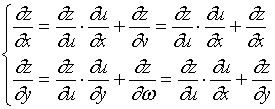
等式两边均出现了![]() 或
或![]() ,尽管记号一样,但其意义有本质的差别,以第一式加以阐明:
,尽管记号一样,但其意义有本质的差别,以第一式加以阐明:
左边的![]() 是将复合函数
是将复合函数![]() 中的
中的![]() 看作常数,而对
看作常数,而对![]() 求偏导数;
求偏导数;
右边的![]() 是把函数
是把函数![]() 中的
中的![]() 及
及![]() 看作常数,而对
看作常数,而对![]() 求偏导数。
求偏导数。
因此,为了避免麻烦, 我们往往将上述两式的形式写为
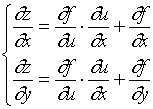

由该复合函数变量间的关系链,可对此求(偏)导数法则作如下解释:
求![]() ,可沿第一条线路对
,可沿第一条线路对![]() 求导, 再沿第二条线路对
求导, 再沿第二条线路对![]() 求导, 最后把两个结果相加。
求导, 最后把两个结果相加。
而沿第一条线路对![]() 求导,相当于把
求导,相当于把![]() 分别视为常量,
分别视为常量,![]() 就成了
就成了![]() 的函数,而
的函数,而![]() 又是
又是![]() 的函数,求导结果自然是
的函数,求导结果自然是![]() ( 这与一元复合函数求导法则很类似);
( 这与一元复合函数求导法则很类似);
而沿第二条线路对![]() 求导,相当于把
求导,相当于把![]() 分别视为常量,
分别视为常量,![]() 就成了
就成了![]() 的函数,而
的函数,而![]() 又是
又是![]() 的函数,求导结果自然是
的函数,求导结果自然是![]() 。
。
上述变量关系图象一根链子,它将变量间的相互依赖关系形象地展示出来。对某个变量求导,就是沿企及该变量的各条线路分别求导,并把结果相加,这一法则称之为锁链法则。
这一法则可简单地概括为
![]()
【例1】设![]() , 而
, 而![]() ,
, ![]() , 求
, 求![]() 和
和![]() 。
。
解: ![]()
![]()
![]()
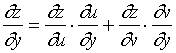
![]()
![]()
【例2】设![]() 而
而![]() ,求
,求![]() 与
与![]() 。
。
解: ![]()
![]()
![]()
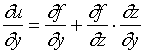
![]()
![]()