§8.5 隐函数的求导公式

一、二元方程所确定的隐函数的情形

由二元方程可确定一个一元的隐函数,将之代入原方程,得到一个恒等式

对恒等式两边关于变量求导,左边是多元复合函数,它对变量的导数为

右边的导数自然为,于是有

解出,得到隐函数的导数 。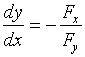

由多元复合函数的求导定理可知,当在具有一阶连续偏导数,而在可导时,才可求出复合函数的导数,若时,才有

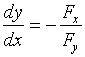
这一求导方法,实际上就是以往的直接求导数。

二、由三元方程所确定的二元隐函数的偏导数

既然二元方程可以确定一个一元的隐函数,那么三元方程便可确定一个二元的隐函数。下面,我们介绍用直接求导法求此函数的偏导数。

对两边关于变量求偏导,并注意是的函数,有

解出,得到二元隐函数的偏导数 。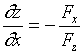

类似地，可得到

, 。

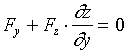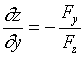【例1】设 , 求 。

解: 将方程中的视为的隐函数,对求偏导数有

再一次对求偏导数,仍然将视为的隐函数有

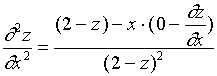
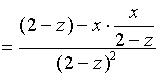
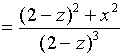
也可以用下述方法来求二阶偏导数

对两边关于求偏导数,注意到均为 的函数,有

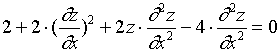
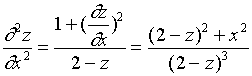
三、由两个函数方程所确定的隐函数的导数

设有函数方程组

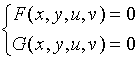
由此联立的方程组可消去一个变量,这样便得到由三个变量所构成的函数方程,而三元函数方程可确定一个二元隐函数 ,将之代入方程组的其中一个,得到另一个三元方程,于是,我们也可将变量表示成的隐函数。

综上讨论,由方程组

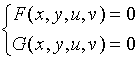
可确定两个二元的隐函数,将之代入上述方程组得到恒等式

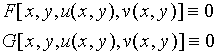
对此恒等式两边关于变量求导,有

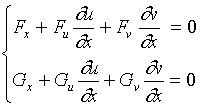
解此关于的方程组,求出 与 。

类似地, 可求出与 。

【例2】设,求及。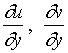

解: 对方程两边关于求导, 注意到是的隐函数, 有

，

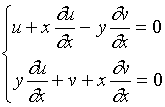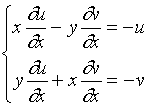
下面解此关于的方程组

将第一式乘以,第二式乘以,再将两式相加得

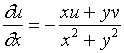
将第一式乘以,第二式乘以,再将两式相减得

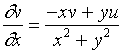
同理,将所给方程对求导有

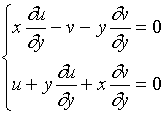
解此方程组得

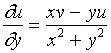
当然,这里自然要求条件 是成立的。