§8.6 微分法在几何上的应用
一、空间曲线的切线与法平面
1、曲线由参数方程给出的情形
设空间曲线![]() 的参数方程为
的参数方程为
![]() (1)
(1)
假定(1)式中的三个函数均可导。
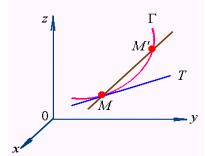
考虑![]() 上对应于
上对应于![]() 的一点
的一点![]() 及对应于
及对应于![]() 的邻近一点
的邻近一点![]() ,其割线
,其割线![]() 的方程为
的方程为
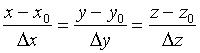
对等式同除以![]() 得
得
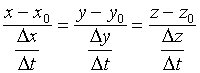
当![]() 时,
时,![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为
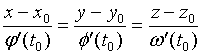 (2)
(2)
这里自然假定了
![]() 不能都为零。
不能都为零。
切线的方向向量称为曲线的切向量,向量
![]()
就是曲线![]() 在点
在点![]() 处的一个切向量。
处的一个切向量。
过点![]() 与切线垂直的平面称为曲线
与切线垂直的平面称为曲线![]() 在点
在点![]() 处的法平面,它是过点
处的法平面,它是过点![]() ,以
,以![]() 为法向量的平面,此法平面方程为
为法向量的平面,此法平面方程为
![]() (3)
(3)
2、曲线由特殊参数方程给出的情形
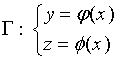 此方程可看作
此方程可看作 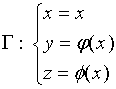
若![]() 在
在![]() 处可导,则
处可导,则![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为
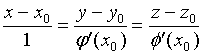 (4)
(4)
曲线![]() 在点
在点![]() 处的法平面方程为
处的法平面方程为
![]() (5)
(5)
3、曲线由一般方程给出的情形
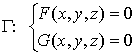
![]() 是曲线上的一点,此函数方程组可确定
是曲线上的一点,此函数方程组可确定![]() 是
是![]() 的隐函数,即曲线可用(隐式)方程
的隐函数,即曲线可用(隐式)方程 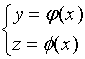 来表示。
来表示。
由第2部分的讨论,现在的关键是求![]() 。
。
将![]() 看作
看作![]() 的隐函数,方程两边分别对
的隐函数,方程两边分别对![]() 求导数,可得
求导数,可得
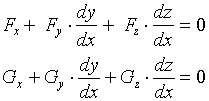 ð
ð 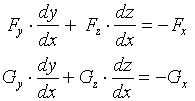
ð 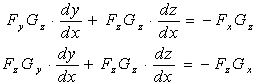
ð ![]()
ð 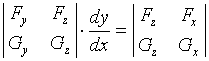 ð
ð 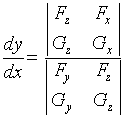
类似地,有
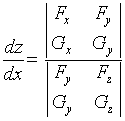
曲线在点![]() 处的切向量本来为
处的切向量本来为![]() ,但也可取向量
,但也可取向量
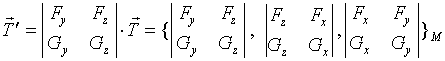
即 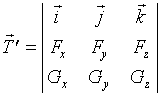
曲线的切线方程为
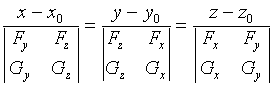 (6)
(6)
曲线的法平面方程为
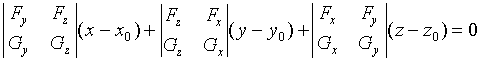 (7)
(7)
当然,上述推导需要一些条件,![]() 具有一阶连续偏导数,且
具有一阶连续偏导数,且
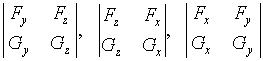
中至少有一个不为零。
【例1】求曲线
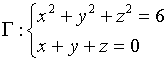
在点![]() 处的切线方程与法平面方程。
处的切线方程与法平面方程。
解: 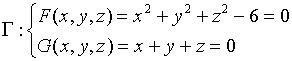
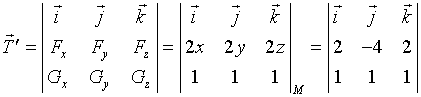
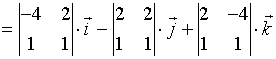
![]()
曲线的切线方程为 ![]()
曲线的法平面方程为 ![]()
二、曲面的切平面与法线
1、曲面方程由![]() 给出的情形
给出的情形
设曲面![]() 由方程
由方程
![]() (9)
(9)
给出,![]() 是
是![]() 上的一点,假设函数
上的一点,假设函数![]() 的偏导数在该点连续且不同时为零。
的偏导数在该点连续且不同时为零。

在![]() 上,过点
上,过点![]() 任意引一条曲线
任意引一条曲线![]() ,设它的参数方程为
,设它的参数方程为
![]()
![]() 对应于参数
对应于参数![]() ,且
,且![]() 不全为零。
不全为零。
则曲线![]() 在点
在点![]() 的切线方程为
的切线方程为
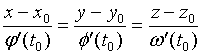
下证事实:
![]() 上过点
上过点![]() 且具有切线的任何曲线 ,它们在点
且具有切线的任何曲线 ,它们在点![]() 处的切线均位于同一平面。
处的切线均位于同一平面。
因为曲线![]() 在曲面
在曲面![]() 上,故有
上,故有
![]()
据假设有 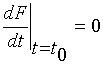 ,即
,即
![]() (10)
(10)
引入向量
![]()
![]()
(10)式表明:![]() 。
。
因为![]() 是过
是过![]() 点且在
点且在![]() 上的任意一条曲线,它们在点
上的任意一条曲线,它们在点![]() 的切线均垂直于同一非零向量
的切线均垂直于同一非零向量![]() ,所以,
,所以,![]() 上过点
上过点![]() 的一切曲线在
的一切曲线在![]() 点的切线都位于同一个平面上。
点的切线都位于同一个平面上。
这个平面称为曲面![]() 在点
在点![]() 的切平面,其切平面方程为
的切平面,其切平面方程为
![]() (11)
(11)
过点![]() 而垂直于切平面(11)的直线称为曲面在该点的法线,其法线方程为:
而垂直于切平面(11)的直线称为曲面在该点的法线,其法线方程为:
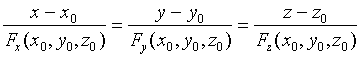 (12)
(12)
曲面在一点的切平面之法向量称为曲面在该点的法向量,因此,向量
![]()
便是曲面![]() 在点
在点![]() 处的一个法向量。
处的一个法向量。
2、曲面方程由![]() 给出的情形
给出的情形
若曲面![]() 由方程
由方程
![]()
给出,令 ![]()
则 ![]()
当偏导数![]() 在点
在点![]() 连续时,曲面在点
连续时,曲面在点![]() 的切平面方程为
的切平面方程为
 (14)
(14)
曲面的法向量有两个
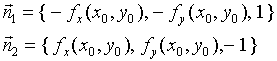
对于第一式,法向量的方向余弦为
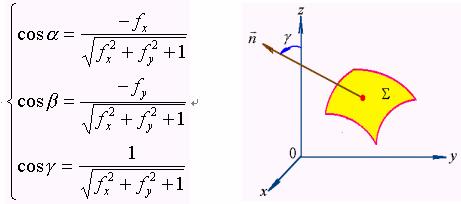
由![]() ,法向量与
,法向量与![]() 轴正向的夹角应为锐角,故此法向量的指向是朝上的。自然地,另一个法向量的指向是朝下的。
轴正向的夹角应为锐角,故此法向量的指向是朝上的。自然地,另一个法向量的指向是朝下的。
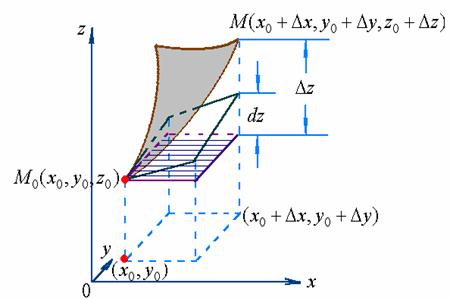
(13)式具有鲜明的几何意义
方程的右端恰好是函数在点![]() 处的全微分;
处的全微分;
方程的左端是切平面上点![]() 的竖坐标的增量。
的竖坐标的增量。
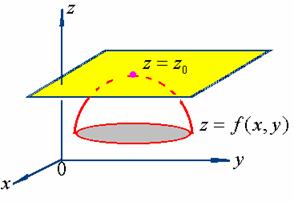
特别地,当 ![]() 时
时
曲面在点![]() 处的切平面为
处的切平面为![]() ,此切平面平行于
,此切平面平行于![]() 坐标面,即曲面在点
坐标面,即曲面在点![]() 处具有水平的切平面。
处具有水平的切平面。
【例2】求球面![]() 在点
在点![]() 处的切平面及法线方程。
处的切平面及法线方程。
解: ![]()
![]()
![]()
切平面方程为
![]()
法线方程为
![]()
因为点![]() 在法线上,可见法线通过球心。
在法线上,可见法线通过球心。