§8.7 方向导数与梯度

一、方向导数

1、定义

设函数在点的某一邻域内有定义,自点引射线,设轴正向到射线的转角为,为邻域内且在上的另一点。

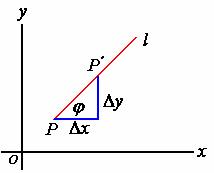
若比值

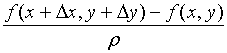
这里,当沿着趋向于时的极限存在,称此极限值为函数在点沿方向的方向导数,记作。

即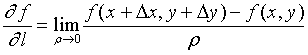

2、方向导数的存在性条件(充分条件)及计算

【定理】若在点可微分, 则函数在该点沿着任一方向的方向导数都存在, 且有

其中为轴正向到方向的转角。

【证明】据在点可微分,有

【例1】求函数在点处沿从点到点的方向的方向导数。

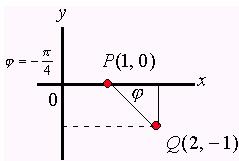
解:轴到方向的转角为，而

在点处，有

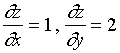
故

注:方向导数的概念及计算公式,可方便地推广到三元函数。

二、梯度

1、定义

设函数在平面区域内具有一阶连续偏导数,那么对于任一点,都可以定义向量

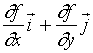
并称此向量为函数在点的梯度,记作。

即

2、方向导数与梯度的关系

设是方向上的单位向量,则

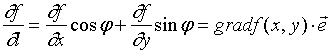
当方向与梯度方向一致时,,从而达到最大值；也就是说, 沿梯度方向的方向导数达到最大值。

另一方面,

这表明:函数在点增长最快的方向与方向导数达到最大的方向(梯度方向)是一致的。

3、等高线及其它

二元函数在几何上表示一个曲面,该曲面被平面所截得的曲线的方程为

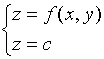
此曲线在面上的投影是一条平面曲线,它们在平面上的方程为。

对于曲线上的一切点, 函数的值都是, 所以,我们称平面曲线为函数的等高线。

【例2】曲面的等高线为 (),

这些等高线为同心圆。

【例3】作抛物线在面上的等高线。

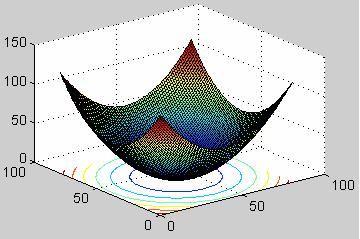
运行matlab程序gs0801.m。