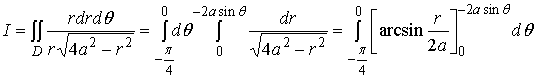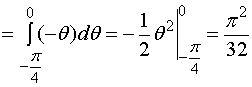§9.2 二重积分的计算法

利用二重积分的定义来计算二重积分显然是不实际的,二重积分的计算是通过两个定积分的计算(即二次积分)来实现的。

一、利用直角坐标计算二重积分

我们用几何观点来讨论二重积分的计算问题。

讨论中,我们假定 ；

假定积分区域可用不等式 表示,

其中, 在上连续。

据二重积分的几何意义可知,的值等于以为底,以曲面为顶的曲顶柱体的体积。

在区间上任意取定一个点,作平行于面的平面,这平面截曲顶柱体所得截面是一个以区间为底,曲线为曲边的曲边梯形,其面积为

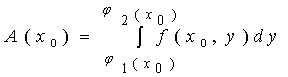
一般地,过区间上任一点且平行于面的平面截曲顶柱体所得截面的面积为

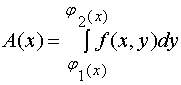
利用计算平行截面面积为已知的立体之体积的方法,该曲顶柱体的体积为

从而有

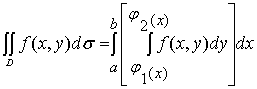(1)

上述积分叫做先对Y,后对X的二次积分,即先把看作常数,只看作的函数,对计算从到的定积分,然后把所得的结果( 它是的函数 )再对从到计算定积分。

这个先对, 后对的二次积分也常记作

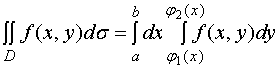
在上述讨论中,假定了，利用二重积分的几何意义,导出了二重积分的计算公式(1)。但实际上,公式(1)并不受此条件限制,对一般的 (在上连续),公式(1)总是成立的。

例如:计算

解: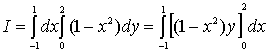

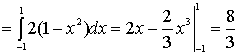
类似地,如果积分区域可以用下述不等式

表示,且函数,在上连续,在上连续,则

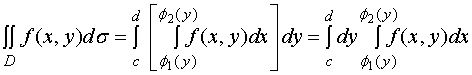(2)

显然,(2)式是先对,后对的二次积分。

二重积分化二次积分时应注意的问题

1、积分区域的形状

前面所画的两类积分区域的形状具有一个共同点:

对于I型(或II型)区域, 用平行于轴(轴 )的直线穿过区域内部,直线与区域的边界相交不多于两点。

如果积分区域不满足这一条件时,可对区域进行剖分,化归为I型(或II型)区域的并集。

2、积分限的确定

二重积分化二次积分, 确定两个定积分的限是关键。这里,我们介绍配置二次积分限的方法 -- 几何法。

画出积分区域的图形(假设的图形如下 )

在上任取一点,过作平行于轴的直线,该直线穿过区域,与区域的边界有两个交点与,这里的、就是将,看作常数而对积分时的下限和上限；又因是在区间上任意取的,所以再将看作变量而对积分时,积分的下限为、上限为。

【例1】计算,其中是由轴,轴和抛物线在第一象限内所围成的区域。

类似地,

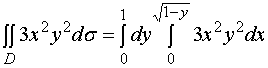
【例2】计算, 其中是由抛物线及直线所围成的区域。

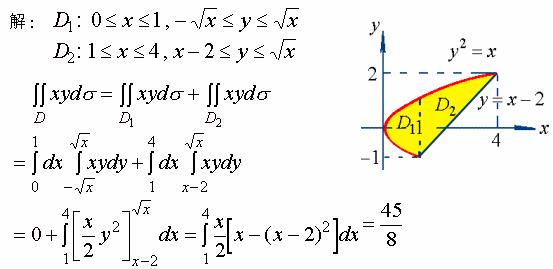
【例3】求由曲面及所围成的立体的体积。

解: 1、作出该立体的简图, 并确定它在面上的投影区域

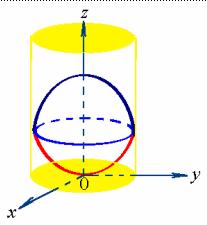
消去变量得一垂直于面的柱面 ,立体镶嵌在其中,立体在面的投影区域就是该柱面在面上所围成的区域

2、列出体积计算的表达式

3、配置积分限, 化二重积分为二次积分并作定积分计算

而

由,的对称性有

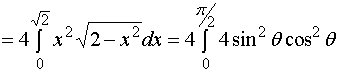
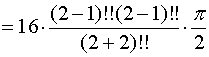
所求立体的体积为

二、利用极坐标计算二重积分

1、变换公式

按照二重积分的定义有

现研究这一和式极限在极坐标中的形式。

用以极点为中心的一族同心圆 以及从极点出发的一族射线 ,将剖分成个小闭区域。

除了包含边界点的一些小闭区域外,小闭区域的面积可如下计算

其中,表示相邻两圆弧半径的平均值。

(数学上可以证明: 包含边界点的那些小闭区域所对应项之和的极限为零, 因此, 这样的一些小区域可以略去不计)

在小区域上取点,设该点直角坐标为,据直角坐标与极坐标的关系有

于是

即

由于也常记作, 因此,上述变换公式也可以写成更富有启发性的形式

(1)

(1)式称之为二重积分由直角坐标变量变换成极坐标变量的变换公式,其中,就是极坐标中的面积元素。

(1)式的记忆方法:

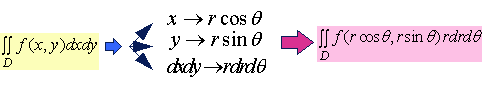
2、极坐标下的二重积分计算法

极坐标系中的二重积分, 同样可以化归为二次积分来计算。

【情形一】积分区域可表示成下述形式

其中函数, 在上连续。

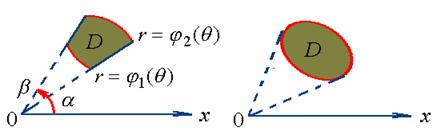
则

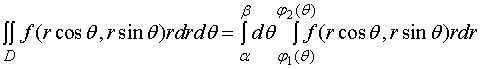
【情形二】积分区域为下述形式

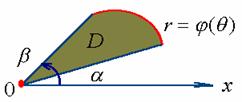
显然,这只是情形一的特殊形式 ( 即极点在积分区域的边界上 )。

故

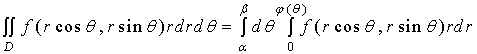
【情形三】积分区域为下述形式

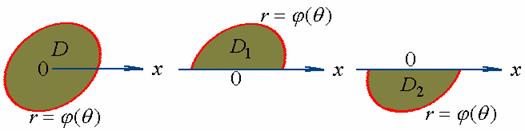
显然,这类区域又是情形二的一种变形( 极点包围在积分区域的内部 ),可剖分成与,而

故

则

由上面的讨论不难发现, 将二重积分化为极坐标形式进行计算, 其关键之处在于: 将积分区域用极坐标变量表示成如下形式

下面通过例子来介绍如何将区域用极坐标变量来表示。

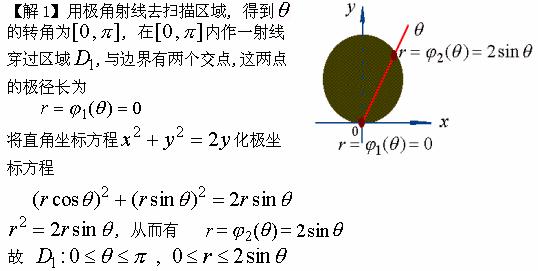
【例4】将下列区域用极坐标变量表示

1、

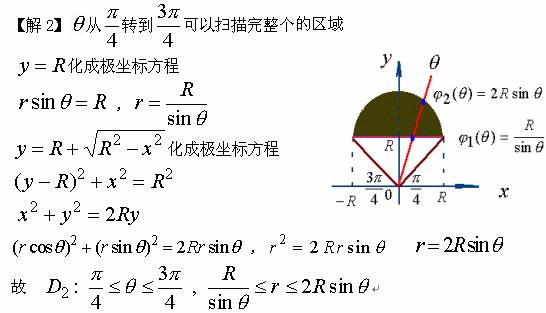
2、

3、

Ê先画出区域的简图, 据图确定极角的最大变化范围；

Ë再过内任一点作射线穿过区域,与区域的边界有两交点,将它们用极坐标表示,这样就得到了极径的变化范围。

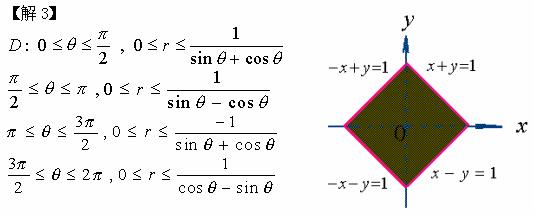
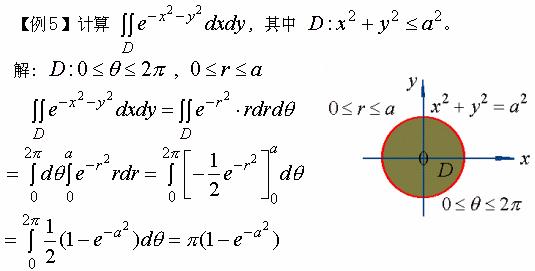
注: 本题不能利用直角坐标下二重积分计算法来求其精确值。

利用此题结果可求出著名概率积分 。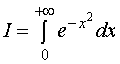

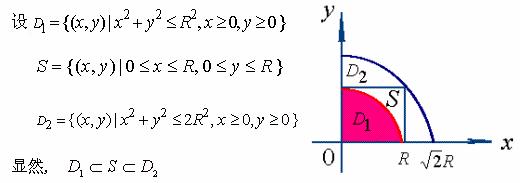
而被积函数满足 ,从而以下不等式

成立，再利用例二的结果有

,

,

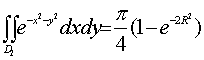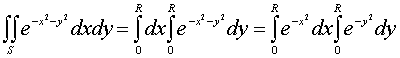
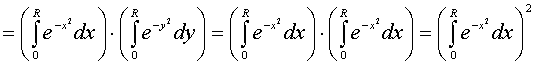
于是不等式可改写成下述形式

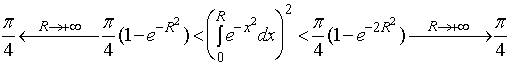
故当 时有 ,

即 。

3、使用极坐标变换计算二重积分的原则

(1)、积分区域的边界曲线易于用极坐标方程表示( 含圆弧,直线段 )；

(2)、被积函数表示式用极坐标变量表示较简单( 含, 为实数 )。

【例6】计算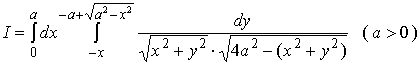

解 此积分区域为

区域的简图为

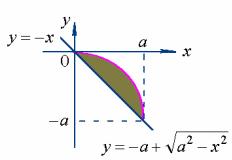
该区域在极坐标下的表示形式为