§9.3 二重积分的应用

定积分应用的元素法也可推广到二重积分,使用该方法需满足以下条件：

1、所要计算的某个量对于闭区域具有可加性(即:当闭区域分成许多小闭区域时, 所求量相应地分成许多部分量,且)。

2、在内任取一个直径充分小的小闭区域时, 相应的部分量可近似地表示为 , 其中, 称为所求量的元素, 并记作。

(注: 的选择标准为: 是直径趋于零时较更高阶的无穷小量)

3、所求量可表示成积分形式

一、曲面的面积

设曲面由方程给出,为曲面在面上的投影区域,函数在上具有连续偏导数和,现计算曲面的面积。

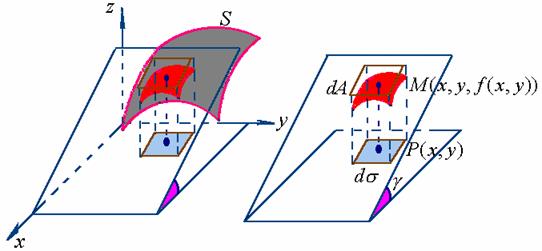
在闭区域上任取一直径很小的闭区域(它的面积也记作),在内取一点,对应着曲面上一点,曲面在点处的切平面设为。 以小区域的边界为准线作母线平行于轴的柱面, 该柱面在曲面上截下一小片曲面,在切平面上截下一小片平面,由于的直径很小,那一小片平面面积近似地等于那一小片曲面面积。

曲面在点处的法线向量( 指向朝上的那个 )为

它与轴正向所成夹角的方向余弦为

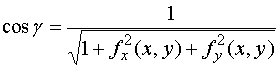
而

所以

这就是曲面的面积元素, 故

故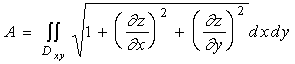

【例1】求球面含在柱面 () 内部的面积。

解:所求曲面在面的投影区域

曲面方程应取为 , 则

,

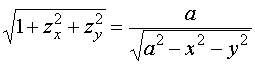
曲面在面上的投影区域为

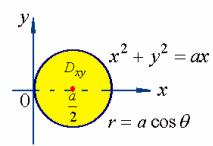
据曲面的对称性,有

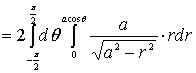
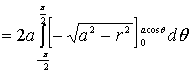
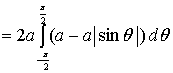
若曲面的方程为或,可分别将曲面投影到面或面,设所得到的投影区域分别为或,类似地有

或

二、平面薄片的重心

1、平面上的质点系的重心

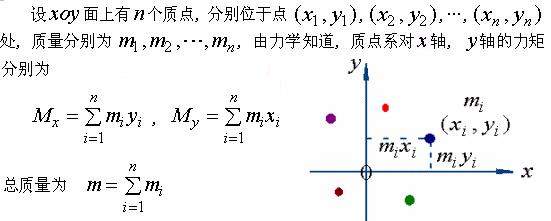
其质点系的重心坐标为

,

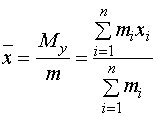2、平面薄片的重心

设有一平面薄片,占有面上的闭区域,在点处的面密度为,假定在上连续,如何确定该薄片的重心坐标。

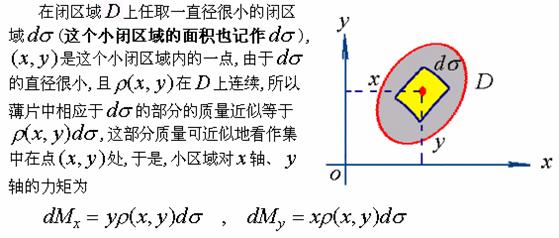
这就是力矩元素,于是

又平面薄片的总质量

从而,薄片的重心坐标为

特别地,如果薄片是均匀的,即面密度为常量,则

十分显然, 这时薄片的重心完全由闭区域的形状所决定, 因此, 习惯上将均匀薄片的重心称之为该平面薄片所占平面图形的形心。

【例2】设薄片所占的闭区域为介于两个圆,

()之间的闭区域,且面密度均匀,求此均匀薄片的重心(形心)。

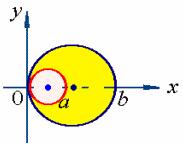
解: 由的对称性可知:

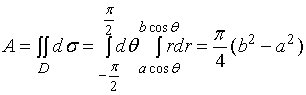
而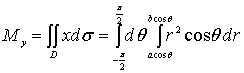

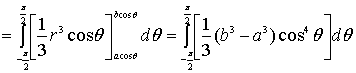
故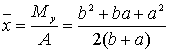

三、平面薄片的转动惯量

1、平面质点系对坐标轴的转动惯量

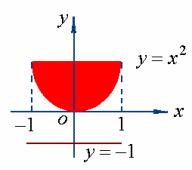
设平面上有个质点, 它们分别位于点处, 质量分别为。

设质点系对于轴以及对于轴的转动惯量依次为

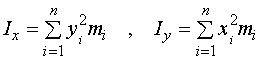
2、平面薄片对于坐标轴的转动惯量

设有一薄片,占有面上的闭区域,在点处的面密度为, 假定在上连续。 现要求该薄片对于轴、轴的转动惯量,。

与平面薄片对坐标轴的力矩相类似,转动惯量元素为

【例3】求由抛物线及直线所围成的均匀薄片(面密度为常数 )对于直线的转动惯量。

解: 转动惯量元素为

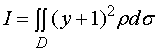
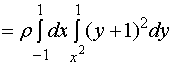
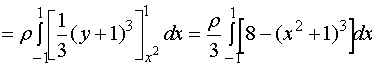
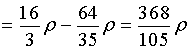
四、平面薄片对质点的引力

设有一平面薄片,占有面上的闭区域,在点 处的面密度为,假定在上连续,现计算该薄片对位于轴上点处的单位质量质点的引力。

于是,薄片对质点的引力在三个坐标轴上的分力的力元素为

故