§9.5 利用柱面坐标和球面坐标计算三重积分

对于某些三重积分,由于积分区域和被积函数的特点,往往要利用柱面坐标和球面坐标来计算。

一、利用柱面坐标计算三重积分

1、柱面坐标

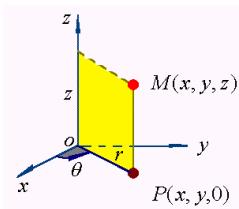
设为空间的一点,该点在面上的投影为,点的极坐标为,则三个数称作点的柱面坐标。

规定的取值范围是

，，

柱面坐标系的三组坐标面分别为

,即以轴为轴的圆柱面；

,即过轴的半平面；

,即与面平行的平面。

点的直角坐标与柱面坐标之间有关系式

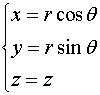(1)

2、三重积分在柱面坐标系中的计算公式

用三组坐标面,,,将分割成许多小区域,除了含的边界点的一些不规则小区域外,这种小闭区域都是柱体。

考察由各取得微小增量所成的柱体,该柱体是底面积为,高为的柱体,其体积为

这便是柱面坐标系下的体积元素, 并注意到(1)式有

(2)

(2)式就是三重积分由直角坐标变量变换成柱面坐标变量的计算公式。

(2)式右端的三重积分计算,也可化为关于积分变量的三次积分,其积分限要由在中的变化情况来确定。

3、用柱面坐标表示积分区域的方法

(1)、找出在面上的投影区域, 并用极坐标变量表示之；

(2)、在内任取一点, 过此点作平行于轴的直线穿过区域, 此直线与边界曲面的两交点之竖坐标( 将此竖坐标表示成的函数 )即为的变化范围。

【例1】求下述立体在柱面坐标下的表示形式

球面与三坐标面所围成的立体且位于第一卦限内的部分。

由锥面与平面所围成的立体。

在面上的投影区域为 ,

其极坐标下的表示形式为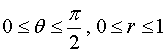

在的变化范围是 ,

即

故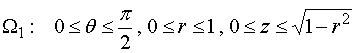

在面上的投影区域为 ,

其极坐标下的表示形式为

在的变化范围是

即

故

【例2】用柱坐标计算三重积分,其中是球体位于第一卦限内的部分。

解:

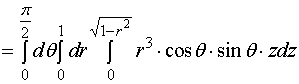
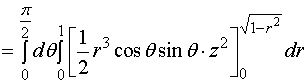
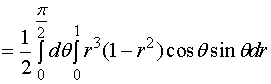
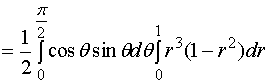
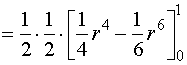
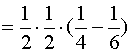
二、利用球坐标计算三重积分

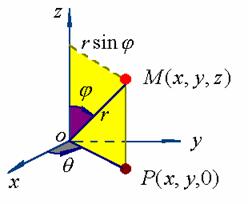
1、球面坐标

如图所示,空间任意一点也可用三个数唯一表示。

其中：

为原点到点的距离；

为有向线段与轴正向所成夹角；

为从正轴来看自轴依逆时针方向转到有向线段的角度,而点是点在面上的投影点。

规定的取值范围为

, ,

不难看出,点的直角坐标与球面坐标间的关系为

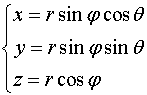(3)

2、球面坐标系的特点

,是以原点为心的球面；

,是以原点为顶, 轴为轴的圆锥面；

,是过轴的半平面。

粗略地讲, 变量刻划点到原点的距离,即“远近”；

变量刻划点在空间的上下位置,即“上下”；

变量刻划点在水平面上的方位,即“水平面上方位”。

3、三重积分在球面坐标系下的计算公式

用三组坐标面, , ,将分划成许多小区域,考虑当各取微小增量 所形成的六面体,若忽略高阶无穷小,可将此六面体视为长方体,其体积近似值为

这就是球面坐标系下的体积元素。

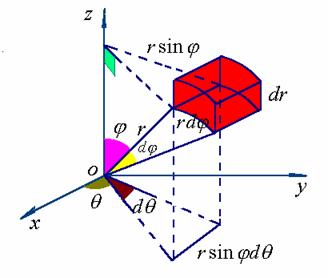
由直角坐标与球面坐标的关系式(3)有

(4)

(4)式就是三重积分在球面坐标系下的计算公式。

(4)式右端的三重积分可化为关于积分变量的三次积分来实现其计算,当然,这需要将积分区域用球面坐标加以表示。

4、积分区域的球面坐标表示法

积分区域用球面坐标加以表示较复杂,一般需要参照的几何形状,并依据球坐标变量的特点来决定。

实际中经常遇到的积分区域是这样的

是一包围原点的立体, 其边界曲面是包围原点在内的封闭曲面,将其边界曲面方程化成球坐标方程,据球面坐标变量的特点有

例如:若是球体 , 则的球坐标表示形式为

曲面的球坐标方程为

于是

【例3】求曲面与曲面所围成的立体的体积。

解:的图形为

下面根据图形及球坐标变量的特点决定的球坐标表示式。

(1)、在面的投影区域包围原点,故变化范围应为；

(2)、在中可由轴转到锥面的侧面,而锥面的半顶角为,故的变化范围应为；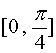

(3)、在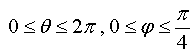 内任取一值, 作射线穿过,它与有两个交点,一个在原点处,另一个在曲面上,它们可分别用球坐标表示为 及 。

因此,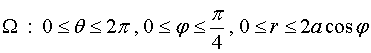

故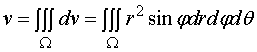

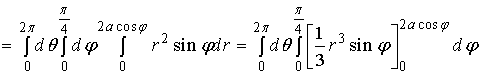
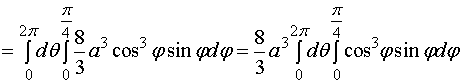
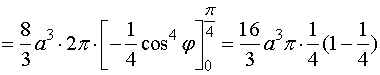
也可以利用柱坐标来计算该立体的体积。
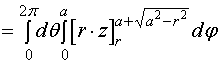
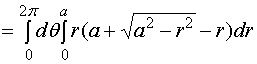
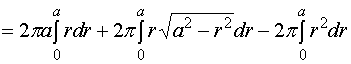
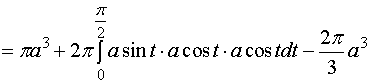
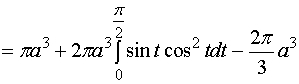
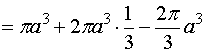