第一章 变量与函数

§1 函数的概念

u 引言：关于函数概念，在中学数学中已有了初步的了解。为便于今后的学习，本节将对此作进一步讨论。

一 变量

变量、常量、实数性质、区间表示

二 函数

１．定义１ 设，如果存在对应法则，使对，存在唯一的一个数与之对应，则称是定义在数集上的函数，记作().也记作。习惯上称自变量，为因变量。函数在点的函数值，记为，全体函数值的集合称为函数的值域，记作。即

。

２．注

（1） 函数有三个要素，即定义域、对应法则和值域。

例：1） （不相同，对应法则相同，定义域不同）

2） （相同，对应法则的表达形式不同）。

（2）函数的记号中的定义域Ｄ可省略不写，而只用对应法则来表示一个函数。即“函数”或“函数”。

（3）“映射”的观点来看，函数本质上是映射，对于，称为映射下的象。称为的原象。

3. 函数的表示方法

1  主要方法：解析法（分式法）、列表法和图象法。

2  可用“特殊方法”来表示的函数。

（１） 分段函数：在定义域的不同部分用不同的公式来表示。

例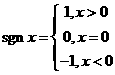：　　，（符号函数）

（２）用语言叙述的函数。

例： １）（的最大整数部分）

２）（Ｄirichlet）

三 函数的一些几何特性

1、单调函数

定义2  设为定义在上的函数， （１）若，则称为上的增函数；若，则称为上的严格增函数。（２）若，则称为上的减函数；若，则称为上的严格减函数。

例：证明：在上是严格增函数。

例：讨论函数在Ｒ上的单调性。

注：单调性与所讨论的区间有关，区间必须关于原点对称。

2、奇函数和偶函数

定义3 设为对称于原点的数集，为定义在上的函数。若对每一个，有（１），则称为Ｄ上的奇函数；（２），则称为上的偶函数。

注：（１）从函数图形上看，奇函数的图象关于原点对称（中心对称），偶函数的图象关于轴对称；

（２）奇偶性的前提是定义域对称；

（３）从奇偶性角度对函数分类：。

3、周期函数

定义4. 设为定义在数集上的函数，若存在，使得对一切有，则称为周期函数，称为的一个周期。

注：（1）若是的周期，则也是的周期，所以周期不唯一。（2）任给一个函数即使存在周期也不一定有最小正周期，如： （Ｃ为常数），任何正数都是它的周期。

§2 复合函数和反函数

一 复合函数

１．引言

先考察一个例子。

例：质量为的物体自由下落，速度为，则功率为

.

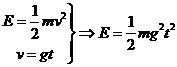我们得到两个函数，把代入，即得

.

这样得到的函数称为“复合函数”。

2． 定义（复合函数） 设有两个函数，若内，则对每一个，通过对应内唯一一个值，而又通过对应唯一一个值，这就确定了一个定义在上的函数，它以为自变量，因变量，记作。这种函数成为复合函数。

注：两个函数能复合，第一个函数的值域必须包含在第二个函数的定义域中。

3. 例子

例： 讨论函数与函数能否进行复合。

4  说明

例：，复合成：.

２）不仅要会复合，更要会分解。

①

二、反函数

１ 反函数概念

设函数。满足：对于值域中的每一个值，中有且只有一个值，使得，则按此对应法则得到一个定义在上的函数，称这个函数为的反函数，记作

.

2  注：

a)  并不是任何函数都有反函数；

b)  函数与互为反函数，并有:

c) ，则函数的反函数通常记为

.

定理．设为严格增（减）函数，则必有反函数，且在其定义域上也是严格增（减）函数。

§3 基本初等函数

一 初等函数

1.．基本初等函数（7类）

常量函数　　（Ｃ为常数）；

幂函数　　；

指数函数；

对数函数　　；

三角函数　　；

反三角函数　　。

双曲函数 ，，，

２．初等函数

定义３．由基本初等函数经过在有限次四则运算与有限次复合运算所得到的函数，统称为初等函数

如：

不是初等函数的函数，称为非初等函数。如Dirichlet函数、Riemann函数、取整函数等都是非初等函数。

例：求函数表为基本初等函数的复合。