第二章 极限与连续
§1 数列的极限与无穷大量
u 引 言
为了掌握变量的变化规律,往往需要从它的变化过程来判断它的变化趋势。例如有这么一个变量,它开始是1,然后为![]() 如此,一直无尽地变下去,虽然无尽止,但它的变化有一个趋势,这个趋势就是在它的变化过程中越来越接近于零。我们就说,这个变量的极限为0。所以,我们有必要对极限作深入研究。
如此,一直无尽地变下去,虽然无尽止,但它的变化有一个趋势,这个趋势就是在它的变化过程中越来越接近于零。我们就说,这个变量的极限为0。所以,我们有必要对极限作深入研究。
一 数列极限的定义
1 数列的定义
定义:若函数![]() 的定义域为全体正整数集合
的定义域为全体正整数集合![]() ,则称
,则称![]() 为数列。
为数列。
注:记![]() ,则数列
,则数列![]() 就可写作为:
就可写作为:![]() ,简记为
,简记为![]() 。
。
2 数列的例子
(1)![]() ;(2)
;(2)![]() (3)
(3)![]()
2、什么是数列极限
1.引言
容易看出,数列![]() 的通项
的通项![]() 随着
随着![]() 的无限增大而无限地接近于零。
的无限增大而无限地接近于零。
一般地说,对于数列![]() ,若当
,若当![]() 无限增大时,
无限增大时,![]() 能无限地接近某一个常数
能无限地接近某一个常数![]() ,则称此数列为收敛数列,常数
,则称此数列为收敛数列,常数![]() 称为它的极限。不具有这种特性的数列就称为发散数列。
称为它的极限。不具有这种特性的数列就称为发散数列。
据此可以说,数列![]() 是收敛数列,0是它的极限。
是收敛数列,0是它的极限。
数列![]() 都是发散的数列。
都是发散的数列。
需要提出的是,上面关于“收敛数列”的说法,并不是严格的定义,而仅是一种“描述性”的说法,如何用数学语言把它精确地定义下来。还有待进一步分析。
以![]() 为例,可观察出该数列具以下特性:
为例,可观察出该数列具以下特性:
随着n的无限增大,![]() 无限地接近于1
无限地接近于1![]() 随着n的无限增大,
随着n的无限增大,![]() 与1的距离无限减少
与1的距离无限减少![]() 随着n的无限增大,
随着n的无限增大,![]() 无限减少
无限减少![]()
![]() 会任意小,只要n充分大。
会任意小,只要n充分大。
如:要使![]() ,只要
,只要![]() 即可;
即可;
要使![]() ,只要
,只要![]() 即可;
即可;
![]()
任给无论多么小的正数![]() ,都会存在数列的一项
,都会存在数列的一项![]() ,从该项之后
,从该项之后![]() ,
,![]() 。即
。即![]() ,当
,当![]() 时,
时,![]() 。
。
如何找N?(或N存在吗?)解上面的数学式子即得:![]() ,取
,取![]() 即可。这样
即可。这样![]() 当
当![]() 时,
时,![]() 。
。
综上所述,数列![]() 的通项
的通项![]() 随
随![]() 的无限增大,
的无限增大,![]() 无限接近于1,即是对任意给定正数
无限接近于1,即是对任意给定正数![]() ,总存在正整数N,当
,总存在正整数N,当![]() 时,有
时,有![]() 。此即
。此即![]() 以1为极限的精确定义,记作
以1为极限的精确定义,记作![]() 或
或![]() 。
。
2.数列极限的定义
定义1
设![]() 为数列,a为实数,若对任给的正数
为数列,a为实数,若对任给的正数![]() ,总存在正整数
,总存在正整数![]() ,使得当
,使得当![]() 时有
时有![]() , 则称数列
, 则称数列![]() 收敛于a, a称为数列
收敛于a, a称为数列![]() 的极限, 并记作
的极限, 并记作![]() 或
或![]() .
.
若数列![]() 没有极限,则称
没有极限,则称![]() 不收敛,或称
不收敛,或称![]() 为发散数列。
为发散数列。
[问题]:如何表述![]() 没有极限?
没有极限?
3。举例说明如何用![]() 定义来验证数列极限
定义来验证数列极限
例: 证明![]() .
.
例: 证明![]() .
.
例:证明 ![]() .
.
例:证明 ![]() .
.
例:证明 ![]() ,其中
,其中![]() .
.
4 关于数列的极限的![]() 定义的几点说明
定义的几点说明
(1)
关于![]() :①
:① ![]() 的任意性;②
的任意性;②![]() 的暂时固定性;③
的暂时固定性;③![]() 的多值性;④正由于
的多值性;④正由于![]() 是任意小正数,我们可以限定
是任意小正数,我们可以限定![]() 小于一个确定的正数。
小于一个确定的正数。
(2) 关于N:① 相应性;②N多值性。
(3) 数列极限的几何理解: “当![]() 时有
时有![]() ”
” ![]() 所有下标大于N的项
所有下标大于N的项![]() 都落在邻域
都落在邻域![]() 内;而在
内;而在![]() 之外,数列
之外,数列![]() 中的项至多只有N个(有限个)。
中的项至多只有N个(有限个)。
(4) 数列极限的等价定义(邻域定义):
定义![]() 任给
任给![]() ,若在
,若在![]() 之外数列
之外数列![]() 中的项只有有限个,则称数列
中的项只有有限个,则称数列![]() 收敛于极限a.
收敛于极限a.
由此可见:数列是否有极限,只与它从某一项之后的变化趋势有关,而与它前面的有限项无关。所以,在讨论数列极限时,可以添加、去掉或改变它的有限项的数值,对收敛性和极限都不会发生影响。
例:证明![]() 都是发散数列。
都是发散数列。
二 无穷小数列
在所有收敛数列中,有一类重要的数列,称为无穷小数列,其定义如下:
定义2 若![]() ,则称
,则称![]() 为无穷小数列。
为无穷小数列。
如![]() 都是无穷小数列。
都是无穷小数列。
数列![]() 收敛于a的充要条件:
收敛于a的充要条件:
定理1 数列![]() 收敛于
收敛于![]() 的充要条件是
的充要条件是![]() 为无穷小数列。
为无穷小数列。
三 收敛数列的性质
性质1(保不等式性)设数列![]() 与
与![]() 均收敛,若存在正数
均收敛,若存在正数![]() ,使得当
,使得当![]() 时有
时有![]() ,则
,则![]() 。
。
性质2(保号性) 若![]() (或
(或![]() ),则对任何
),则对任何![]() (或
(或![]() ),存在正数N,使得当
),存在正数N,使得当![]() 时有
时有![]() (或
(或![]() )。
)。
性质3(极限唯一性) 若数列![]() 收敛,则它只有一个极限。
收敛,则它只有一个极限。
性质4(迫敛性) 设收敛数列![]() 、
、![]() 都以a为极限,数列
都以a为极限,数列![]() 满足:存在正数
满足:存在正数![]() ,当
,当![]() 时有
时有![]() ,则数列
,则数列![]() 收敛,且
收敛,且![]() .
.
注:迫敛性不仅给出了判定数列收敛的一种方法,而且也提供了一个求数列极限的工具。
例: 求数列![]() 的极限。
的极限。
性质5(有界性)若数列![]() 收敛,则
收敛,则![]() 为有界数列。
为有界数列。
注:数列收敛则必有界,反之未必。例如数列![]() 有界,但它不收敛。
有界,但它不收敛。
四 数列极限的运算
性质6(极限的四则运算法则) 若![]() 、
、![]() 为收敛数列,则
为收敛数列,则![]() 也都收敛,且有
也都收敛,且有
![]() ;
;
![]() .
.
若再做假设![]() 及
及![]() ,则数列
,则数列![]() 也收敛,且有
也收敛,且有
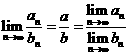 .
.
在求数列的极限时,常需要使用极限的四则运算法则。
例: 求![]() ,其中
,其中![]() .
.
例: 求![]() 。
。
五 单调有界数列
在研究比较复杂的极限问题时,通常分两步来解决:先判断该数列是否有极限(极限的存在性问题);若有极限,再考虑如何计算些极限(极限值的计算问题)。这是极限理论的两基本问题。下面将重点讨论极限的存在性问题。
定义 若数列![]() 的各项满足不等式
的各项满足不等式![]() ,则称
,则称![]() 为递增(递减)数列。递增和递减数列统称为单调数列.
为递增(递减)数列。递增和递减数列统称为单调数列.
例如:![]() 为递减数列;
为递减数列;![]() 为递增数列。
为递增数列。
定理(单调有界定理) 在实数系中,有界且单调数列必有极限。
例:设![]() 其中
其中![]() ,证明数列
,证明数列![]() 收敛。
收敛。
例:证明下列数列收敛,并求其极限:
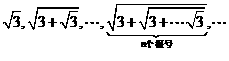
例:证明![]() 存在。
存在。
六 无穷大量的定义
定义:设![]() 是一个数列。若
是一个数列。若![]() 当
当![]() 时必有
时必有![]() ,则称
,则称![]() 是无穷大量。
是无穷大量。
几何解析:
例:证明 是无穷大量。
是无穷大量。
定义:设![]() 是一个数列。若
是一个数列。若![]() 当
当![]() 时必有
时必有![]() ,则称
,则称![]() 是正无穷大量。
是正无穷大量。
定义:设![]() 是一个数列。若
是一个数列。若![]() 当
当![]() 时必有
时必有![]() ,则称
,则称![]() 是负无穷大量。
是负无穷大量。
七 无穷大量的性质和运算
1、 无穷大量和无穷小量的关系
定理:![]() 为无穷大量,当且仅当,
为无穷大量,当且仅当,![]() 为无穷小量,这里要求
为无穷小量,这里要求![]() 。
。
2、 无穷大量的一些运算法则
定理:正无穷大量的和仍是正无穷大量,负无穷大量的和仍是负无穷大量。无穷大量加上有界数列仍是无穷大量。
定理:设![]() 为无穷大量,
为无穷大量,![]() 收敛于
收敛于![]() ,则
,则![]() 是无穷大量。
是无穷大量。
§2 函数的极限
一 函数在一点的极限
现在讨论当![]() 时,对应的函数值能否趋于某个定数A数列。
时,对应的函数值能否趋于某个定数A数列。
先看下面几个例子:
例: ![]() 。当
。当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() )。
)。
由上例可见,对有些函数,当![]() 时,对应的函数值
时,对应的函数值![]() 能趋于某个定数A;但对有些函数却无此性质。所以有必要来研究当
能趋于某个定数A;但对有些函数却无此性质。所以有必要来研究当![]() 时,
时,![]() 的变化趋势。
的变化趋势。
定义1 设函数![]() 在点
在点![]() 的附近有定义,A为定数,若对任给的
的附近有定义,A为定数,若对任给的![]() ,使得当
,使得当![]() 时有
时有![]() ,则称称A为
,则称称A为![]() 时
时![]() 的极限,记作
的极限,记作![]() 或
或![]() .
.
注:(1)![]() 是结论,
是结论,![]() 是条件,即由
是条件,即由![]() 推出。
推出。
(2)![]() 是表示函数
是表示函数![]() 与A的接近程度的。
与A的接近程度的。
(3) ![]() 是表示
是表示![]() 与
与![]() 的接近程度,它相当于数列极限的
的接近程度,它相当于数列极限的![]() 定义中的N。它的第一个特性是相应性。第二个特性是多值性。
定义中的N。它的第一个特性是相应性。第二个特性是多值性。
(4)在定义中,只要求函数![]() 在
在![]() 的某空心邻域内有定义,而一般不要求
的某空心邻域内有定义,而一般不要求![]() 在
在![]() 处的函数值是否存在,或者取什么样的值。
处的函数值是否存在,或者取什么样的值。
(5)定义的几何意义。
例:证明 ![]() ;
;
二 函数极限的性质和运算
性质1(局部保号性)若![]() ,则对任何正数
,则对任何正数![]() ,存在
,存在![]() ,当
,当![]() 时,有
时,有![]() ;若
;若![]() ,则对任何负数
,则对任何负数![]() ,存在
,存在![]() ,当
,当![]() 时有
时有![]() 。
。
性质2(保不等式性)设![]() 和
和![]() 都存在,且存在
都存在,且存在![]() ,当
,当![]() 时,有
时,有![]() 。
。
性质3(唯一性) 若极限![]() 存在,则此极限是唯一的。
存在,则此极限是唯一的。
性质4(迫敛性) 设![]() ,且存在
,且存在![]() ,当
,当![]() 时有
时有![]() ,则
,则![]() 。
。
性质5(局部有界性)若![]() 存在,则
存在,则![]() 在
在![]() 的某空心邻域内有界。
的某空心邻域内有界。
性质6(海涅定理)![]()
![]() 都有
都有![]() 。
。
性质7(四则运算法则)若![]() 和
和![]() 都存在,则函数
都存在,则函数![]() 当
当![]() 时极限也存在,且
时极限也存在,且
1)![]() ;
;
2)![]() .
.
又若![]() ,则
,则![]() 当
当![]() 时极限也存在,且有 3)
时极限也存在,且有 3)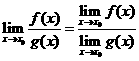 。
。
性质8 无穷小量乘有界变量仍是无穷小量。
三 单侧极限
1.引言
有些函数在其定义域上某些点左侧与右侧的解析式不同,如

或函数在某些点仅在其一侧有定义,如
![]() 。
。
这时,如何讨论这类函数在上述各点处的极限呢?
定义2设函数![]() 在点
在点![]() 的有近旁有定义,A为定数,若对任给的
的有近旁有定义,A为定数,若对任给的![]() ,使得当
,使得当![]() 时有
时有![]() ,则称数A为函数
,则称数A为函数![]() 当
当![]() 趋于
趋于![]() 时的右极限,记作
时的右极限,记作
![]() 或
或![]() 或
或![]() 。
。
类似可给出左极限定义。
注:右极限与左极限统称为单侧极限。
例: 讨论函数![]() 在
在![]() 的左、右极限。
的左、右极限。
例: 讨论![]() 在
在![]() 的左、右极限。
的左、右极限。
函数极限![]() 与
与![]() 的关系。
的关系。
定理1 ![]() .
.
注:利用此可验证函数极限的存在。
四 函数在无限远处的极限
定义3 设![]() 为定义在
为定义在![]() 上的函数,A为实数。若对任给的
上的函数,A为实数。若对任给的![]() ,存在正数
,存在正数![]()
![]() ,使得当
,使得当![]() 时有
时有 ![]() , 则称函数
, 则称函数![]() 当
当![]() 时以A为极限。记作
时以A为极限。记作
![]() 或
或![]() .
.
类似可定义![]() 和
和![]() 。
。
注:![]()
![]()
![]() 。
。
例: 按定义证明![]() .
.
例: 按定义证明1)![]() ;2)
;2)![]() .
.
五 函数值趋于无穷大的情形
定义4 设函数![]() 在点
在点![]() 的附近有定义,若对任给的
的附近有定义,若对任给的![]() ,使得当
,使得当![]() 时有
时有![]() ,则称
,则称![]() 在点
在点![]() 时趋于无穷大,记作
时趋于无穷大,记作![]() 。
。
类似可定义![]() ,
,![]() ,
,![]() 。
。
六 两个常用的不等式和两个重要的极限
1、 ![]() 的证明
的证明
2、![]() 的应用
的应用
例:求![]() .
.
例:求![]() .
.
注:利用归结原则,可求数列极限。如求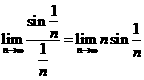 ,直接利用
,直接利用![]() 是不严格的;但已知
是不严格的;但已知![]() ,故取
,故取![]() ,则
,则![]() ,从而由归结原则
,从而由归结原则 .
.
例:求![]() .
.
3、证明![]() 或
或![]() .
.
4、 应用
例:烈求![]() .
.
例:求![]() .
.
例:求![]() .
.
§3 连续函数
l 引言
在数学分析中,要研究种种不同性质的函数,其中有一类重要的函数,就是连续函数。下面我们就来研究这类函数的特点。
一 连续的定义
定义1(![]() 在点
在点![]() 连续)设函数
连续)设函数![]() 在某
在某![]() 点的附近包括
点的附近包括![]() 点有定义,若
点有定义,若![]() ,则称
,则称![]() 在点
在点![]() 连续。
连续。
注 ![]() ,即“
,即“![]() 在点
在点![]() 连续”意味着“极限运算与对应法则
连续”意味着“极限运算与对应法则![]() 可交换。
可交换。
例:![]() 在
在![]() 处连续。
处连续。
例:![]() 。
。
例:讨论函数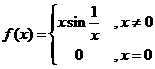 在点x=0处连续性。
在点x=0处连续性。
注:1)设![]() ,
,![]() ——函数
——函数![]() 在点
在点![]() 的增量。
的增量。
2)等价定义1:函数![]() 在点
在点![]() 连续
连续![]()
![]() 。
。
3) 等价定义2:函数![]() 在点
在点![]() 连续
连续![]()
![]() ,当
,当![]() 时,
时,![]() 。
。
注:一个定义是等价的,根据具体的问题选用不同的表述方式。
总的来讲,函数在点![]() 连续的要求是:①
连续的要求是:①![]() 在点
在点![]() 有定义;②
有定义;②![]() 存在;③
存在;③![]() . 任何一条不满足,
. 任何一条不满足,![]() 在点
在点![]() 就不连续。同时,由定义可知,函数在某点是可连续,是函数在这点的局部性质。
就不连续。同时,由定义可知,函数在某点是可连续,是函数在这点的局部性质。
5.![]() 在点
在点![]() 左(右)连续定义
左(右)连续定义
① 定义2设函数![]() 在点
在点![]() 点的右(左)近旁包括
点的右(左)近旁包括![]() 点有定义,若
点有定义,若![]() (
(![]() ),则称
),则称![]() 在点
在点![]() 右(左)连续。
右(左)连续。
② ![]() 在点
在点![]() 连续的等价刻划
连续的等价刻划
定理1 函数![]() 在点
在点![]() 连续
连续![]()
![]() 在点
在点![]() 既是右连续,又是左连续。
既是右连续,又是左连续。
例:讨论函数![]() 在点
在点![]() 的连续性。
的连续性。
二 连续函数的性质和运算
定理2(四则运算)若![]() 和
和![]() 在
在![]() 点连续,则
点连续,则![]() 也都在点
也都在点![]() 连续。
连续。
问题 两个不连续函数或者一个连续而另一个不连续的函数的和、积、商是否仍旧连续?
定理3(复合函数的连续性)若![]() 在点
在点![]() 连续,记
连续,记![]() ,函数
,函数![]() 在
在![]() 连续,则复合函数
连续,则复合函数![]() 在点
在点![]() 连续。
连续。
注
1) 据连续性定义,上述定理可表为:![]() .(即函数运算与极限可以交换次序,条件是函数连续,利用它可来求一些函数的极限。)
.(即函数运算与极限可以交换次序,条件是函数连续,利用它可来求一些函数的极限。)
三 初等函数的连续性
定理4 任何初等函数都是在其定义区间上的连续函数。
定理5 一切基本初等函数都是其定义域上连续函数。
2.利用初等函数的连续性可计算极限
例:设![]() ,
,![]() ,证明:
,证明:![]() 。
。
例:求![]() 。
。
四 不连续点的类型
不连续点分类
1) 可移不连续点 若![]() ,而
,而![]() 在点
在点![]() 无定义,或有定义但
无定义,或有定义但![]() ,则称
,则称![]() 为
为![]() 的可去间断点。
的可去间断点。
例如:![]() 是函数
是函数![]() 的可移不连续点。
的可移不连续点。
设![]() 是
是![]() 的可移不连续点,且
的可移不连续点,且![]() 。令
。令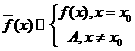 ,则
,则![]() 是
是![]() 的连续点。
的连续点。
2) 第一类不连续点 若![]() 存在,但左右极限不相等,则称点
存在,但左右极限不相等,则称点![]() 为函数
为函数![]() 的第一类不连续点。
的第一类不连续点。
例如,对![]() ,
,![]() 故
故![]() 是它的第一类不连续点。
是它的第一类不连续点。
3) 第二类不连续点 左右极限至少有一不存在的点(即函数至少有一侧极限不存在的点)称为函数的第二类不连续点。
例如,![]() 是函数
是函数![]() ,
,![]() 的第二类不连续点。
的第二类不连续点。
五 区间上连续函数的基本性质
性质1(最大、最小值定理)若![]() 在闭区间
在闭区间![]() 上连续,则
上连续,则![]() 在
在![]() 上有最大值与最小值。
上有最大值与最小值。
性质2(有界性定理)若![]() 在
在![]() 上连续,则
上连续,则![]() 在
在![]() 上有界。
上有界。
注:上述性质成立的条件是充分的,而非必要的。
性质3(介值定理)设![]() 在
在![]() 上连续,且
上连续,且![]() 。若
。若![]() 是介于
是介于![]() 和
和![]() 之间的任何实数,则至少存在一点
之间的任何实数,则至少存在一点![]() ,使得
,使得![]() 。
。
注 表明若![]() 在
在![]() 上连续,又
上连续,又![]() 的话,则
的话,则![]() 在
在![]() 上可以取得
上可以取得![]() 和
和![]() 之间的一切值。
之间的一切值。
性质4(根存在定理) 若![]() 在
在![]() 上连续,且
上连续,且![]() 和
和![]() 异号(
异号(![]() ),则至少存在一点
),则至少存在一点![]() ,使得
,使得![]() 。
。
几何意义 若点![]() 和
和![]() 分别在
分别在![]() 轴两侧,则连接A、B的曲线
轴两侧,则连接A、B的曲线![]() 与
与![]() 轴至少有一个交点。
轴至少有一个交点。
例:设![]() 在
在![]() 上连续,满足
上连续,满足![]() 。证明:存在
。证明:存在![]() ,使得
,使得![]() 。
。
提示:构造适当的![]() ;构造适当的闭区间。
;构造适当的闭区间。
六 一致连续性
1.一致连续的定义
定义3(一致连续) 设![]() 为定义在区间
为定义在区间![]() 上的函数。若对任给的
上的函数。若对任给的![]() ,存在一个
,存在一个![]() ,使得对任何
,使得对任何![]() ,只要
,只要![]() ,就有
,就有![]() ,则称函数
,则称函数![]() 在区间
在区间![]() 上一致连续。
上一致连续。
2.函数在区间上连续与一致连续的比较
(1) 区别:
|
定义 |
函数 |
函数 |
|
对 |
对于 |
|
|
性质 |
与区间中每一点及其附近的 |
要知 |
(2) 关系
若![]() 在
在![]() 上一致连续,则
上一致连续,则![]() 在
在![]() 上连续;反之不成立。
上连续;反之不成立。
定理(康托Cantor定理) 若函数![]() 在闭区间
在闭区间![]() 上连续,则
上连续,则![]() 在
在![]() 上一致连续。
上一致连续。
例:证明 ![]() 在
在![]() 上一致连续。
上一致连续。
例:(1)证明函数![]() 在
在![]() 内不一致连续。
内不一致连续。
(2)![]() ,证明
,证明 ![]() 在
在![]() 内是一致连续的。
内是一致连续的。
§4 无穷小量与无穷大量的阶
两个无穷小量,哪一个收敛速度更快呢?。
定义1 设当![]() 时,
时,![]() 均为无穷小量。
均为无穷小量。
1) 若![]() ,则称
,则称![]() 为
为![]() 的高阶无穷小量,记作
的高阶无穷小量,记作![]() ;
;
2)若![]() ,则称
,则称![]() 为
为![]() 的同阶无穷小量,记作
的同阶无穷小量,记作![]() 。
。
3)若![]() ,则称
,则称![]() 和
和![]() 为等价无穷小量,记作
为等价无穷小量,记作![]() 。
。
4)若![]() ,则称
,则称![]() 为
为![]() 阶无穷小量,称
阶无穷小量,称![]() 为
为![]() 的主要部分。
的主要部分。
注:可类似定义无穷大量。
例:求当![]() 时,
时,![]() 的阶和主要部分。
的阶和主要部分。
注:在求极限过程中,可利用等价无穷小量代换求极限,但应注意:只有对所求极限式中相乘或相除的因式才能用等价无穷小量来替代,而对极限式中相加或相减的部分则不能随意替代。
例:求极限![]() 。
。