第四章 导数与微分
§1 导数的引进和定义
一 导数的引进
1． 引言（背景）
来看两个实际问题。
问题1 已知曲线求它的切线：曲线方程
，
是其上一点，求过点
的切线方程。
问题2 已知运算规律，求物体运动速度，运动规律：
，
为某一确定时刻，求质点在时刻的速度。
上述两问题中，第一个是几何学的问题，后一个是物理学问题，但问题都归结到求形如
的极限问题。
二、导数的定义及几何意义
定义1（导数） 设函数在
的某邻域内有定义，若极限
存在，则称函数
在点处可导，并称该极限为在点处的导数，记作
。即
。
若上述极限不存在，则称在点处不可导。
1. 利用导数定义求导数的几个例子
例：求
在点
处的导数。
2． 可导与连续的连续
定理1 若函数在点可导，则在点连续。
注 若在点不连续，则在必不可导。但在点连续，未必有在可导。
3． 单侧导数的概念
定义2 （右导数） 设函数在点的某右邻域
上有定义，若右极限
存在，则称该极限为在点的右导数，记作
。
左导数 
。
左、右导数统称为单侧导数。
4. 可导函数
若函数在区间I上每一点都可导（对区间端点，仅考虑单侧导数），则称为I上的可导函数。
5. 导函数
6. 函数在点的导数与导函数的区别与联系
区别：导数是就一点而言的，是一个确定的数，一般与所给函数以及的值均有关，与
无关；导函数是就一个区间而言的，是一个确定的函数，与所给函数有关，与
、均无关。
联系：函数在某点的导数就是导函数在该点的值，因此，在的导数也记为：
，
，
。
7 导数与左、右导数的关系：
定理2 若函数在点的某邻域内有定义，则存在
，
都存在，且=。
例: 设
讨论
在
处的左、右导数与导数。
注 讨论分段函数在分段点处的导数，应用导数的定义。
8. 导数的几何意义
表示
点
的切线的斜率。
例: 求曲线
在点
处的切线方程与法线方程。
§2 简单函数的导数
一 常数的导数
。
二 三角函数的导数
；
三 对数函数的导数
。
四 幂函数的导数
。
例 按定义证明，可导的偶函数其导函数是奇函数。
§3 求导法则
一、 导数的四则运算
一般地，有如下的求导法则：
定理1（和差的运算法则） 若
，
可导，则函数
也可导，且 
。
例：
，求
，
。
定理2（积的运算法则）若，可导，则函数
也可导，且
。
例：
，求
。
定理3（数乘的运算法则）若可导，则函数
也可导，
。
定理4（相除的运算法则） 若函数，可导，且
，则
也可导，且
。
例3：设
，求。
二 反函数的导数
定理5 设为
的反函数，若
在点
的某邻域内连续，严格单调且
，则在点（
）可导，且
。
注：反函数的倒数等于原函数的倒数份之一。
例：
（
）；
例：
例：
，
。
§4 复合函数求导法
一 复合函数的导数
定理1. 设
在点
可导，
在点可导，则复合函数
在点可导，且
。
例：
，求
。
例：
设
，求，
。
例：
设
，其中
且和均可导，试求此幂指函数的导数。（对数求导法）
例：
设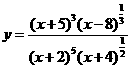 
（
），求
。
§5 微分及其运算
一 微分的定义
1．引言
先考察一个具体的问题，推得一般情形。
2．微分的定义
定义1 函数
定义在点
的某邻域
内。当给一个增量，
时，相应地得到函数的增量为
。如果存在常数
，使得
能有
（1）
则称函数在点可微，并称（1）中右端第一项
为在点的微分，记作：
or 
定义2 若在区间
上每一点都可微，则称为上的可微函数。函数在上任一点处的微分记作
， 
。
注：（1）
依赖于和，但与无关是两个相互独立的变量。
可微与可导的关系：
定理1 函数f在点可微f在点可导，而且
。
注：（3）
，所以微分
。
（4）对可导函数，有
，从而有
，即函数的导数是函数微分与自变量微分的商（导数即微商）。
二 微分的运算法则
（1）
；（2）
；
（3）
；（4）
，其中。
注 在（4）中，由于
，
。即（4）式：
不仅在为自变量时成立，当它是另一个可微函数的因变量时也成立。这性质成为一阶微分的形式不变性。
例：求
的微分。
例：求
的微分。
§6 隐函数及参数方程所表示函数的求导法
一 隐函数求导法
设
，
为的函数，等式两边对求导，得
。
从而
。
例：设
，求
。
二 参数方程所表示函数的求导法
设函数
由参数方程
确定，其中
是参数，则
.
例：求
所确定的函数在
时的导数。
例：求下面由参数方程所确定的函数的导数，
。
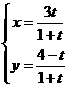在
处。
注 分清求导的对象，即到底是关于哪个变量求导。
§7 不可到的函数举例
例：
在不可导。
例：求函数
在
点的左导数和右导数。
注：处处连续但处处不可导的函数是存在的。
§8 高阶导数与高阶微分
一 高阶导数及其运算法则
定义 若函数的导函数
在点可导，则称在点的导数为在点的二阶导数，记作
，
或
。
函数的二阶导数
一般仍旧是的函数。如果对它再求导数，如果导数存在的话，称之为函数的三阶导数，记为
，
，或
。
函数的
阶导数的导数称为函数的
阶导数，记为
，
，或
。
二阶及二阶以上的导数都称为高阶导数。
从高阶导数的定义可知，求高阶导数无非是反复运用求一阶导数的方法。
例：求幂函数
的各阶导数。
一般地，任何首项系数为1的多项式：
的阶导数为
，
阶导数为零。
例：
。
例：
，
，则
；
。
高阶导数的计算法则
1． 
。
2．
， （Leibniz公式）
其中
，
。
注 将Leibniz公式与二项式展开作一比较可见：
。（这里 
），在形式上二者有相似之处。
从定义出发，重复应用一阶导数法则，容易建立“复合函数”的高阶导数，“参数方程”的高阶导数公式。但这些公式非常繁，对于求高阶导数没有多大帮助，因此不作深入讨论。
作为例子，我们指出参数方程求二阶导数的方法。
设
，
在[
]上都是二阶可导，则由参数方程所确定的函数的一阶导数
。则
。
例：试求由摆线参量方程
所确定的函数的二阶导数。
二 高阶微分
对于函数
，类似于高阶导数，可以定义高阶微分，具体做法如下：
二阶微分定义为
称之为函数的二阶微分。记作
or 
。
一般地，阶微分是
阶微分的微分，记作
，即
注 （1）
； 
是x的二阶微分（=0）；
是
的微分（一阶）（＝
）；（2）
是n阶导数记法的来由；（3）一阶微分具有形式不变性，对于高阶微分已不具备此性质，以二阶微分为例。若，则（ⅰ）当x为自变量时，；（ⅱ）当为因变量，如
时，
。
例：记
，
，分别求
，（1）当是自变量时，（2）当是因变量时。