第六章 不定积分

§1  不定积分概念与运算法则

微分法的基本问题——从已知函数求出它的导数；但在某些实际问题中，往往需要考虑与之相反的问题——求一个已知函数，使其导数恰好是某一已知函数——这就是所谓的积分问题。

一 原函数与不定积分

定义1 设函数与在区间上有定义。若

， ，

则称为在区间上的一个原函数。

如：是在R上的一个原函数；等都是在R上的原函数——若函数存在原函数，则其原函数不是唯一的。

问题1 在什么条件下必存在原函数？若存在，其个数是否唯一；又若不唯一，则有多少个？

问题2 若函数的原函数存在，如何将它求出？

定理1 设是在在区间上的一个原函数，则（1）设是在在区间上的原函数，其中C为任意常量（若存在原函数，则其个数必为无穷多个）。（2）在上的任何两个原函数之间，只可能相差一个常数。

定义2  函数在区间上的原函数的全体称为在上的不定积分，记作：

其中积分号；被积函数； 被积表达式；积分变量。

注: 是一个整体记号；

注：不定积分与原函数是总体与个体的关系，即若是的一个原函数，则的不定积分是一个函数族，其中是任意常数，于是，记为：=。

此时称为积分常数，它可取任意实数。故有

——先积后导正好还原；

——先导后积还原后需加上一个常数（不能完全还原）。

如： 。

不定积分的几何意义：若是的一个原函数，则称的图象为的一条积分曲线。于是，的不定积分在几何上表示的某一条积分曲线沿纵轴方向任意平移所得一组积分曲线组成的曲线族。

结论：若在每一条积分曲线上横坐标相同的点处作切线，则这些切线互相平行。

二 不定积分的基本公式

由于不定积分的定义不象导数定义那样具有构造性，这就使得求原函数的问题要比求导数难得多，因此，我们只能先按照微分法的已知结果去试探。首先，我们把基本导数公式改写成基本积分公式：

1.；2.；3.，；

4.，；5.；

6.， ；7.，；

8.，；9.；

10.；11.；

12.；13.；

14.。

牢记上述基本积分公式。

三 不定积分的运算法则

定理2 若函数与在区间上都存在原函数，为两个任意常数，则 也存在原函数，且（积分的线性）。

注：线性法则的一般形式为： 。

例：求。

例： 求。

例：求

§2  不定积分的计算

一 “凑”微分法

有一些不定积分，将积分变量进行一定的变换后就能有基本的积分公式求出所需的积分。

例：求。

例：求。

例：求。

注：为了求积分，把它凑成如下的形式，作代换，于是有，如果这个积分可在基本积分公式中查到为，再代回原来的变量，就求得积分。

二 换元积分法

定理1 （换元积分法） 设连续，及皆为连续，的反函数存在且连续，并且

，

则

。

注：在换元积分法中是将被积函数的某一部分视为一个整体看作一个新的积分变量。

例：求 。

例：求 。

例：求 。

使用换元积分法的关键：在于把被积表达式凑成形式，从而作变换，化积分为：。但要注意的是最后要换回原积分变量。

例：求 。

三 分部积分法

定理2（分部积分法） 若与可导，不定积分存在，则不定积分也存在，且

，

即

。

例：求 。

例：求 。

例：求和.

四 有理函数积分法

定义：设和是两个多项式，凡形如

的函数称为有理函数。

重要结论：任何一个有理函数必定可以表示为若干个形如（称为简单分式）：

（1） ； （2） ；

（3）； （4）。

的简单分式之和，其中A，B，为常数，为正整数。

因此，对有理函数的积分只要讨论上述四种形式的积分即可。

（1） 。

（2） ， 。

（3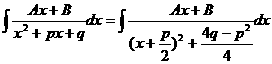） ，令，并记，，则

。

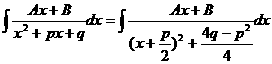
（4） 同（3）可得 ，

。

记 ，则

               =

，

于是，有递推公式

。

将这些结果代回，即可求得所求积分。

例：求。

例：求。

五 其他类型的积分举例

1、形如 的积分

只要令就可有理化。

例： 求 。

例：求 。

2、形如的积分

把积分分成两项

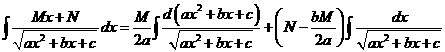
右边的积分即可求出，第二个积分配成完全平方，使成为

。

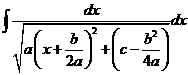例：求。

3、形如的积分

把积分分成两项

右边的积分即可求出，第二个积分配成完全平方，使成为

或

的积分。

例：求

4、 形如的积分

对于三角有理式的不定积分，一般通过变换（万能变换），可把它化为有理函数的积分：

；

； ；

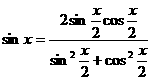
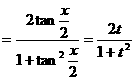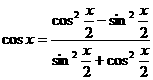
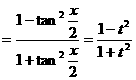故 。

例：求 。

注意：上述变换对三角有理式的不定积分总是有效的，但并不一定是最好的变换，在实际计算中要注意选择不同的变换。

例：求 。

注意：初等函数的原函数不一定是初等函数，因此，在初等函数的范围内，某些初等函数的原函数是不存在的，即使该函数可积。