第七章 定积分

§1  定积分的概念

一 问题的提出

不定积分和定积分是积分学中的两大基本问题，求不定积分是求导数的逆运算，而定积分则是某种特殊和式的极限，它们之间既有本质的区别，但也有紧密的联系。先看下面的例子。

1．曲边梯形的面积 设函数在闭区间上连续，且。则由曲线，直线，以及轴所围成的平面图形（如下左图），称为曲边梯形。下面将讨论该曲边梯形的面积（这是求任何曲线边界图形的面积的基础）。

在区间内任取个分点，依次为

它们将区间分割成个小区间，。记为，即，。并用表示区间的长度，记，再用直线，把曲边梯形分割成个小曲边梯形。在每个小区间，上任取一点，，作以为高，为底的小矩形，其面积为，当分点不断增多，又分割得较细密时，由于连续，它在每个小区间上的变化不大，从而可用这些小矩形的面积近似代替相应的小曲边梯形的面积。于是，该 曲边梯形面积的近似值为。从而

。

二 定积分的定义

定义1 设是定义在[]上的一个函数，在内插入若干个分点（这里插入个），依次为

，

将闭区间[]分成个小区间，记为，，简，任取点，，并作和式。又设是一个确定的实数，若对任给的，总存在，使得对[]的任意分割，以及，，只要，就有

。

则称函数在[]上可积或黎曼可积。数称为函数在[]上的定积分或黎曼积分，记作：

其中称为被积函数，称为积分变量，[]称为积分区间，称为被积式，分别称为积分的下限和上限。

定理：若在可积，则在必定有界。

定积分的几何意义：定积分的几何意义就是-------由连续曲线及直线所围曲边梯形的面积。

注：定积分的值只与被积函数及积分区间[]有关，而与积分变量所用的符号无关。

规定：及。

例：利用定积分的定义计算积分：。

§2定积分存在的条件

一 定积分存在的充分必要条件

定义1 设函数在有界，在插入分点

把分成个小区间，记

作和式

分别成为对于这一分法的达布上和达布下和。

要判断一个函数是否可积，由定义，可直接考察积分和是否能无限接近某一常数，但由于积分和的复杂性和那个常数不可预知，因此这是极其困难的。下面即将出的可积准则只与被积函数本身有关，而不涉及定积分的值。

定理1（定积分存在的第一充分必要条件） 函数在上可积的充分必要条件是。

注：定理1也可叙述为函数在上可积的充分必要条件是。

例：证明

在不可积，但。

定义2 记，称之为在上的幅度，则有

。

注：定理1也可叙述为函数在上可积的充分必要条件是。

定理2 （定积分存在的第二充分必要条件） 函数在上可积的充分必要条件是对任意的两个正数及，可找到，使当任一分法满足时，对应于幅度的那些区间的长度之和。

注：定理揭示了可积函数的本质，表明可积函数不连续的范围不能太广。

二 可积函数类

定理3 若函数为上的连续函数，则在上可积。

定理4 若是区间上只有有限个第一类不连续点的有界函数，则在上可积。

定理5 若是区间上的单调函数，则在上可积。

注意：单调函数即使有无限多个间断点，也仍然可积。

例：试用两种方法证明函数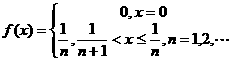在区间上可积。

§3  定积分的性质

性质1 若函数在上可积，为常数，则在上也可积，且

。

即常数因子可从积分号里提出（注意与不定积分的不同）。

性质2 若函数、都在上可积，则在上也可积，且有

。

性质3 若函数、都在上可积，则在上也可积。

注意：一般地 。

性质4 若函数在上可积，则也在上可积

注：性质4的你不对。例如

在不可积，但。

性质5（关于积分区间的可加性） 函数在上可积，在与上都可积，此时有。

注：性质5对的任何大小顺序都成立。

性质6 设函数在上可积，且，，则。

例：设函数在上连续，，，且在不恒等于0，证明。

性质7 若函数在上可积，则。

性质8（积分第一中值定理）若在上连续，在上不变号且可积，则至少存在一点，使得。

说明：当时，结论为则至少存在一点，使得。

注：事实上，积分第一中值定理中的点必能。

积分第一中值定理的几何意义：如右图，若在上非负连续，则在上的曲边梯形的面积等于以为高，为底的矩形的面积。

一般地，称为在上的平均值。

例：试求在上的平均值。

性质9 若在上可积，则在上连续。

§4  定积分的计算

一 定积分计算的基本公式

定理1 若函数在上连续，则在上处处可导，且，。

说明：此定理沟通了导数与定积分之间的关系；同时也证明了连续函数必有原函数这一结论，并以积分的形式给出了的一个原函数。因此，该定理也称之为微积分学基本定理。且用它可以给出牛顿-莱布尼茨公式的另一证明。

用定义来计算定积分一般是很困难的，下面将要介绍的牛顿—莱布尼茨公式不仅为定积分的计算提供了一个有效的方法，而且在理论上把定积分与不定积分联系了起来。

定理2 若函数在上连续，且存在原函数，则在上可积，且

这即为牛顿—莱布尼茨公式，也常记为。

注：在实际应用中，定理的条件是可以适当减弱的，如只要在在上可积即可。

例：计算下列定积分：

1）（n为整数）；

 2）（0<a<b）；

3）。

二 定积分的换元积分法

定理3（定积分的换元积分法）若函数在上连续，作代换。其中在上有连续导数，当时，且，则

。

注意：在应用中要注意定积分的换元公式与不定积分的换元公式的异同之处。

例：求。

例：求。

例：求。

三 定积分的分部积分法

定理4（定积分的分部积分法）若、为上的连续可微函数，则

，

或 。

例：求。

例：求。

四 杂例

注：因为定积分是一类和式的极限，故可以借助于定积分来为某些特殊的极限。

例：利用定积分求极限： 。

例：求。

例：设在上连续，那么当是偶函数时，；当是奇函数时，。