第八章 定积分的应用
§1 平面图形的面积
如果一块图形是由连续曲线![]() ,
,![]() 以及
以及![]() ,
,![]() 所围成,那么这块图形的面积的计算公式为
所围成,那么这块图形的面积的计算公式为
![]() 。
。
例:求![]() ,
,![]() 所围的面积
所围的面积![]() 。
。
例:求![]() ,
,![]() 在
在![]() 上所围图形的面积。
上所围图形的面积。
若所给的曲线方程为参数形式:![]() (
(![]() ),其中
),其中![]() 是连续函数,
是连续函数,![]() 是连续可微函数,且
是连续可微函数,且![]() 且
且![]() ,
,![]() ,那么由
,那么由![]() ,
,![]() 轴及直线
轴及直线![]() 所围图形的面积S的公式为
所围图形的面积S的公式为
![]() (
(![]() )。
)。
例:求旋轮线:![]() 一个拱与
一个拱与![]() 轴所围的图形的面积。
轴所围的图形的面积。
例:求椭圆![]() (
(![]() ,
,![]() )的面积
)的面积![]() 。
。
设曲线的极坐标方程是:![]() ,
,![]() ,
,![]() ,则由曲线
,则由曲线![]() ,射线
,射线![]() 及
及![]() 所围的扇形面积
所围的扇形面积![]() 等于
等于
![]() 。
。
例:求双纽线![]() 所围图形面积
所围图形面积![]() 。
。
例:求由![]() ,
,![]() ,所决定的外层曲线和内层曲线之间的面积
,所决定的外层曲线和内层曲线之间的面积![]() 。
。
§2 曲线的弧长
1、先建立曲线的长度(弧长)的概念
一条线段的长度可直接度量,但一条曲线段的“长度”一般却不能直接度量,因此需用不同的方法来求。
设平面曲线![]() 由参数方程
由参数方程![]() (
(![]() )给出,设
)给出,设![]() 是[
是[![]() ]的一个划分[
]的一个划分[![]() ],即
],即![]() ,它们在曲线
,它们在曲线![]() 上所对应的点为
上所对应的点为![]() ,
,![]() ,…,
,…,![]() 。从端点
。从端点![]() 开始用线段一次连接这些分点
开始用线段一次连接这些分点![]() ,
,![]() ,…,
,…,![]() 得到曲线的一条内接折线,用
得到曲线的一条内接折线,用![]() 来表示
来表示![]() 的长度,则内接折线总长度为
的长度,则内接折线总长度为
![]()
曲线![]() 的弧长
的弧长![]() 定义为内接折线的总长在
定义为内接折线的总长在![]() 时的极限:
时的极限:
![]()
如果![]() 存在且为有限,则称
存在且为有限,则称![]() 为可求长曲线。
为可求长曲线。
2、弧长公式
设曲线![]() :
:![]() (
(![]() ),且
),且![]() ,
,![]() 在[
在[![]() ]上可微且导数
]上可微且导数![]() ,
,![]() 在[
在[![]() ]上可积,曲线
]上可积,曲线![]() 在[
在[![]() ]无自交点,则曲线
]无自交点,则曲线![]() 的弧长
的弧长![]() 为:
为:
![]()
注:其它形式的弧长公式
(1)设![]() 在
在![]() 上可微且导数
上可微且导数![]() 可积,则曲线
可积,则曲线![]() (
(![]() )的弧长
)的弧长![]() 为:
为:
![]() 。
。
(2)若曲线极坐标方程![]() ,
,![]() ,则当
,则当![]() 在[
在[![]() ]上可微,且
]上可微,且![]() 可积时,
可积时,
![]() 。
。
例:求圆周![]() ,
,![]() ,
,![]() 的弧长
的弧长![]() 。
。
例:求抛物线![]() ,
,![]() 的弧长
的弧长![]() 。
。
例3、求椭圆![]() (
(![]() )的弧长
)的弧长![]() 。
。
3、弧长的微分
设![]() :
:![]() (
(![]() )是光滑曲线,
)是光滑曲线,![]() ,
,![]() 在[
在[![]() ]连续且
]连续且![]() +
+![]() ),且无自交点。若把公式中的积分上限
),且无自交点。若把公式中的积分上限![]() 改为
改为![]() ,就得到曲线
,就得到曲线![]() ,由端点
,由端点![]() 到动点
到动点![]() 的一段弧长为
的一段弧长为
![]()
由上限函数的可微性知![]() 存在,
存在,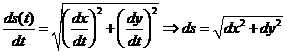 。
。
§3 体积
一 一般体积公式
设一几何体夹在![]() 和
和![]() (
(![]() )这两个平行平面之间,用垂直于
)这两个平行平面之间,用垂直于![]() 轴的平面去截此几何体,设载面与
轴的平面去截此几何体,设载面与![]() 轴交点为
轴交点为![]() ,可得的截面面积为
,可得的截面面积为![]() ,如果
,如果![]() 是
是![]() 上的黎曼可积函数,则该几何体的体积V等于
上的黎曼可积函数,则该几何体的体积V等于
![]() 。
。
例:求![]() 及
及![]() 的体积
的体积![]() 。
。
例:求由椭球面![]() 所围的几何体体积
所围的几何体体积![]() 。
。
二 旋转体的体积
设![]() ,
,![]() 是一条连续曲线,曲线
是一条连续曲线,曲线![]() ,
,![]() 绕
绕![]() 轴产生旋转体的截面积为
轴产生旋转体的截面积为![]() =
=![]() ,则
,则
![]() =
=![]()
例:求抛物线![]() ,
,![]() 分别绕
分别绕![]() 轴和
轴和![]() 轴所产生的旋转体体积。
轴所产生的旋转体体积。
§4 旋转曲面的面积
设![]() 在
在![]() 上非负,且连续可微,该曲线绕
上非负,且连续可微,该曲线绕![]() 轴旋转后所得的旋转面的侧面积为
轴旋转后所得的旋转面的侧面积为
![]()
例:求半径为![]() 的球面面积
的球面面积![]() 。
。
例:某反光镜可近似地看成介于![]() 与
与![]() 米之间的抛物线
米之间的抛物线![]() 绕
绕![]() 轴旋转所成的旋转抛物面。求此反光镜镜面的面积。
轴旋转所成的旋转抛物面。求此反光镜镜面的面积。
§5 质心
重心在计算不少实际问题中遇到,例如造船时就要考虑怎样来设计才使船的重心低一些。设在平面上有![]() 个质点,质点坐标为
个质点,质点坐标为![]() ,原量分别为
,原量分别为![]() ,则该重心为(
,则该重心为(![]() ),有以下公式:
),有以下公式:
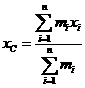 ,
,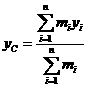 。
。
定义:均匀物体的重心也叫做形心。
下面将此概念加以推广,来计算一般平面曲线(弧)的原心:
设曲线![]() 方程为
方程为![]() (
(![]() ),
),![]() ,
,![]() 存在且
存在且![]() ,则曲线
,则曲线![]() 的重心坐标(
的重心坐标(![]() )有近似公式:
)有近似公式:
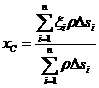 ,
,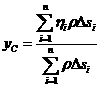 。
。
记![]() ,则
,则![]() 时,得
时,得
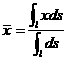 ,
,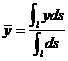 。
。
具体地,如果曲线方程段为![]() ,(
,(![]() ),
),![]() 在
在![]() 连续,则此曲线段的质心坐标为
连续,则此曲线段的质心坐标为
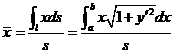 ,
,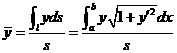 。
。
其中![]() 为曲线段的弧长。如果密度不是常数,而是
为曲线段的弧长。如果密度不是常数,而是![]() 的连续函数
的连续函数![]() ,(
,(![]() )那么完全类似地可得曲线段质心坐标为:
)那么完全类似地可得曲线段质心坐标为:
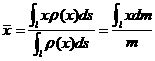 ,
,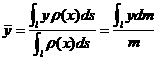
其中![]() ,
,![]() 为曲线段的质量。
为曲线段的质量。
例:求以r为半径的半圆弧的形心。
例:轴长10米,密度分布为![]() 千克/米,其中
千克/米,其中![]() 为距轴的一个端点的距离,求轴之质量。
为距轴的一个端点的距离,求轴之质量。
§6 平均值、功
一 平均值
设![]() 在闭区间
在闭区间![]() 连续,把区间
连续,把区间![]() 等分,分点为
等分,分点为
![]()
每一个分点![]() 上的函数值是
上的函数值是![]()
![]() ,分点间的距离时
,分点间的距离时![]() ,则
,则![]() 的算术平均值为
的算术平均值为
![]()
令![]() ,则得
,则得![]() 在
在![]() 上的平均值为
上的平均值为
![]() 。
。
例:求![]() 在
在![]() 上的平均值。
上的平均值。
例:求交流电的平均功率。
二 功
设物体在力![]() 的作用下从
的作用下从![]() 点运动到
点运动到![]() 点,则
点,则![]() 在
在![]() 上所作的功为
上所作的功为![]() 。
。
例:求力![]() 从0运动到10所作的功。
从0运动到10所作的功。
例:半径为![]() 的球沉入水中,它与水面相接,球的比重为
的球沉入水中,它与水面相接,球的比重为![]() ,现将球从水中取出,要作多少功?
,现将球从水中取出,要作多少功?
§7 定积分的近似计算
设![]() 在区间
在区间![]() 上连续,将区间分成
上连续,将区间分成![]() 个相等的区间,分点为
个相等的区间,分点为
![]() ,
,
令![]() ,则Simpson公式为
,则Simpson公式为
![]() 。
。