第九章 数 项 级 数

§1 预备知识：上极限和下极限

对于一个有界数列，去掉他的最初项以后，剩下来的依旧是一个有界数列，记

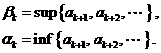
显然，数列是单调减少的，是单调增加的，所以这两个数列的极限存在。称的极限是的上极限，设它为。称的极限是的下极限，设它为。记为

显然：。

定理1  设

则（i）当为有限时，对于的任何邻域，在数列中有无穷多个项属于这个邻域，而在只有有限多个项。

（ii）当时，对任何数，在中波有无穷多项大于。

（iii）当时，数列以为极限。

定理2  设

则（i）当为有限时，对于的任何邻域，在数列中有无穷多个项属于这个邻域，而在只有有限多个项。

（ii）当时，对任何数，在中波有无穷多项小于。

（iii）当时，数列以为极限。

定理3  设为的上极限，那么，必是中所有收敛子列的极限中的最大值。设为的下极限，那么，必是中所有收敛子列的极限中的最小值。

推论1 的充分必要条件为

。

例：设，求它的上下极限。

例：设，求它的上下极限。

§2 级数的收敛性及其基本性质

一 级数概念

在初等数学中，我们知道：任意有限个实数相加，其结果仍是一个实数，在本章将讨论——无限多个实数相加——级数——所可能出现的情形及特征。如

从直观上可知，其和为1。

又如， 。 其和无意义；

若将其改写为： 则其和为：0；

若写为： 则和为：1。（其结果完全不同）。

问题：无限多个实数相加是否存在和；

如果存在，和等于什么。

定义1 给定一个数列，将它的各项依次用加号“+”连接起来的表达式

（1）

称为数项级数或无穷级数（简称级数），其中称为级数（1）的通项。级数记为：。

二 级数的收敛性

记 ，称之为级数的前项部分和，简称部分和。

定义2 若数项级数的部分和数列收敛于（即），则称数项级数收敛 ，记作

=。

若部分和数列发散，则称数项级数发散。当级数收敛时，又称

为级数的余和。

注：无穷级数的收敛问题，实质上是部分和数列的收敛问题。

例: 试讨论等比级数（几何级数）

，

的收敛性。

例:讨论级数

的收敛性。

三 收敛级数的性质

性质1 若级数都有收敛，则对任意常数，级数也收敛，且

。

性质2 若级数与都有收敛，则级数也收敛，且

。

即对于收敛级数来说，交换律和结合律成立。

性质3 在收敛级数的项中任意加括号，既不改变级数的收敛性，也不改变它的和。

注意：从级数加括号后的收敛，不能推断加括号前的级数也收敛（即去括号法则不成立）。

如：

收敛，而级数

是发散的。

性质4  （收敛的必要条件）若级数收敛，则。

注：只是级数收敛的必要条件，不是充分条件。

例：级数发散，但。

敛散性是由它的部分和数列来确定的，因而也可以认为数项级数是数列的另一表现形式。反之，对于任意的数列，总可视其为数项级数

的部分和数列，此时数列与级数有

相同的敛散性，因此，有

定理1（Cauchy收敛原理） 级数收敛的充要条件是：任给正数，总存在正整数，使得当以及对任意的正整数，都有

。

注：级数发散的充要条件是：存在某个，对任何正整数N，总存在正整数，有

。

例：利用收敛原理来判断级数的收敛性。

例：利用收敛原理来判断调和级数的收敛性。

§3 正 项 级 数

一 正项级数收敛性的一般判别原则

若级数各项的符号都相同，则称为同号级数。而对于同号级数，只须研究各项都由非负项数组成的级数——正项级数。因负项级数同正项级数仅相差一个负号，而这并不影响其收敛性。

基本定理 正项级数收敛部分和数列有上界。

正项级数的比较判别法

定理1设和均为正项级数，如果存在某个正数N，使得对都有

，

那么（1）若级数收敛，则级数也收敛；

（2）若级数发散，则级数也发散。

例: 考察的收敛性。

推论（比较判别法的极限形式） 设和是两个正项级数，若

，

则 （1） 当时，级数、同时收敛或同时发散；

（2）当且级数收敛时，级数也收敛；

（3）当且发散时，级数也发散。

例: 讨论级数 的收敛性。

例: 讨论级数的收敛性。

柯西判别法

定理2 设为正项级数，且存在某个正整数及正常数，

（1）若对，有，则级数收敛；

（2）若对，有，则级数发散。

推论（柯西判别法的极限形式）设为正项级数，且

，

则 （1）当时，级数收敛；

（2）当（可为）时，级数发散；

（3）当时，级数可能收敛，也可能发散。如：，。

例：讨论级数 的敛散性。

达朗贝尔判别法

定理3设为正项级数，且存在某个正整数及常数：

（1） 若对，有 ，则级数收敛 ；

（2） 若对，有 ，则级数发散。

推论 设为正项级数，且

，

则（1）当时，级数收敛；

（2） 当（可为）时，级数发散；

（3） 当时，级数可能收敛，也可能发散。如：，。

例：讨论级数的收敛性。

例：讨论级数的收敛性。

说明：因 ，这就说明凡能用达朗贝尔判别法判定收敛性的级数，也能用柯西判别法来判断，即柯西判别法较之达朗贝尔判别法更有效。但反之不能。

柯西积分判别法

定理4 设为[上非负减函数，则正项级数与反常积分同时收敛或同时发散。

例: 讨论下列级数

（1） ，（2），

的敛散性。

§4   任意项级数

一 绝对收敛级数

定义1 若级数各项绝对值所组成的级数收敛，则称原级数绝对收敛。若级数收敛，但级数发散，则称级数条件收敛。

定理1 绝对收敛的级数一定收敛。但反之不然。

注：例如.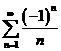

说明：对于级数是否绝对收敛，可用正项级数的各判别法进行判别。

例：对任何实数，级数 是绝对收敛的。

若级数收敛，但级数发散，则称级数条件收敛。

例：是条件收敛的；和是绝对收敛的。

全体收敛的级数可分为绝对收敛级数和条件收敛级数两大类。

二 交错级数

定义2 若级数的各项符号正负相间，即

，

称为交错级数。

定理2（莱布尼茨判别法） 若交错级数满足下述两个条件：

（1） 数列单调递减； （2）。

则级数收敛。且此时有。

推论 若级数满足莱布尼茨判别法的条件，则其余和估计式为

。

例：判别下列级数的收敛性：（1）；（2）；（3）。

三 阿贝耳判别法和狄立克莱判别法

定理3（阿贝尔判别法）若为单调有界数列，且级数收敛，则级数

收敛。

例：根据阿贝尔判别法法可知，当级数收敛时，级数

，

收敛。

定理4（狄立克莱判别法）若为单调递减数列，且，又级数的部分和数列有界，则级数

收敛。

例：若数列为单调递减，且，则级数

，

对任何都收敛。

§5   绝对收敛技术和条件收敛级数的性质

定理1 对于级数，令

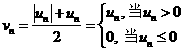
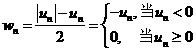
那么：（i）若级数绝对收敛，则级数和都收敛。

（ii）若级数条件收敛，则级数和都发散。

定义1  对于一个级数，他的更序级数就是把它的项重新排列后所得到的级数。

定理2 绝对收敛级数的更序级数仍为绝对收敛，且其和相同，= 。

定理3 若级数条件收敛，那么，总可以适当地更换原来级数的次序而组成一个级数，使它收敛于任何预先给定的数（包括的情形）。

注：（1）由条件收敛的级数重排后所得到的级数，不一定收敛；即使收敛，也不一定收敛于原来的和数。

如：设 ，

则 ，

而 ，

它正是第1个级数的重排。

级数的乘积

设有收敛级数

， （1）

。 （2）

它们每一项所有可能的乘积为：

… …

… …

… … （3）

… … … … … …

… …

… … … … … …

定理4（柯西定理） 若级数（1）、（2）都绝对收敛，则对（3）中所有乘积按任意顺序排列所得到的级数也绝对收敛，且和等于AB。

例：等比级数

=，

是绝对收敛的，将按（3）的顺序排列。则得到

=

                = .

注：（3）中所有乘积可以按各种方法排成不同的级数，常用的有按正方形顺序：

；

或对角线顺序：

。 （4）

定义2 称级数（4）为两级数和的柯西乘积。

例：证明 = 。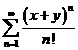