第十章 广义积分

§1 无穷限的广义积分

定积分有两个明显的缺陷：其一，积分区间是有限区间；其二，若，则，使得对于任意的，（即有界是可积的必要条件）。这两个缺陷限制了定积分的应用，因为在许多实际问题和理论问题中都要去掉这两个限制，把定积分的概念拓广为：

（i）无限区间上的积分；（ii）无界函数的积分。

一、无穷限广义积分的概念

定义1  设在上有定义，且对于任意的在区间上可积。当极限

存在时，称这极限值为在上的广义积分。记作

。

如果上述的极限不存在，就称发散。

类似可定义。

当和都收敛时，就称收敛，并且有

。

这是显然有：

。

如果上述的极限不存在，就称发散。

定理1  如果在连续，是的原函数，则

。

例：讨论的收敛情形。

无穷限积分的性质

性质1 若函数在上可积，为常数，则在上也可积，且

。

即常数因子可从积分号里提出（注意与不定积分的不同）。

性质2 若函数、都在上可积，则在上也可积，且有

。

性质3  对无穷限积分，分布积分和换元积分法则也成立。

柯西收敛原理 收敛的充分必要条件是：，，当时，总有。

定义2  若积分收敛，就称绝对收敛。收敛但不绝对收敛的积分成为条件收敛。

定理2  绝对收敛的广义积分必收敛。但反之不然。

二 无穷限广义积分的收敛性判别法

1、比较判别法

设从某一值起起，常有，而积分收敛，那么积分绝对收敛；又如果，而积分发散，那么积分发散。

2、比较判别法的极限形式

如果

，

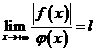则 （1） 当时，且收敛，那么积分绝对收敛；

（2）当时，且发散，那么积分发散。

3、柯西判别法

如果，，那么绝对收敛；又如果，而积分发散，那么积分发散。

定理2 如果，，那么绝对收敛；如果，，自某一值起就保持定号，那么积分发散。

4、柯西判别法的极限形式

如果

，

则 （1） 当时，，那么积分绝对收敛；

（2）当时，，那么积分发散。

例: 讨论广义积分的敛散性。

例: 讨论广义积分的敛散性。

例: 讨论广义积分的敛散性。

§2 无界函数的广义积分

一 无穷限广义积分的概念

定义1  设在的临近无界（我们称点为的奇点），但对于任意充分小的正数，在上可积，即

存在时，称这极限值为无界函数在上的广义积分。记作

。

如果上述的极限不存在，就称发散。

类似可定义（为奇点）。

如果在内部有一个奇点，，当和都收敛时，就称收敛，并且有

。

如果上式右边的任何一个积分发散，就称发散。

例：讨论积分的收敛性。

例：讨论积分的收敛性。

无穷限积分的性质

性质1 定积分的一些性质包括分部积分法和换元积分法对无界函数的广义积分也成立。

柯西收敛原理 （是奇点）收敛的充分必要条件是：，，当时，总有。

定义2  若积分（是奇点）收敛，就称绝对收敛。收敛但不绝对收敛的积分成为条件收敛。

定理2  绝对收敛的广义积分必收敛。但反之不然。

二 无界函数广义积分的收敛性判别法

1、柯西判别法

设是的奇点，如果，，那么绝对收敛。如果，，那么发散。

2、柯西判别法的极限形式

如果

，

则（1）当时，，那么积分绝对收敛；

（2）当时，，那么积分发散。

例：求下列广义积分：，。

例：讨论广义积分的收敛性。

定义3 设在内无界，是唯一的奇点。如果

存在，我们就称此极限为广义积分的柯西主值，记为

。

同样，对于无穷限的广义积分，柯西主值为

例：设，求的主值。

例：求的主值。