第十一章 函数项级数、幂级数

§1  函数项级数的一致收敛

我们知道，可以用收敛数列（或级数）来表示或定义一个数，下面将讨论如何用函数列（或函数项级数）来表示或定义一个函数。

一 函数项级数的概念

设是定义在数集上的一个函数列，表达式

， （1）

称为定义在上的函数项级数，记为。称

， ， （2）

为函数顶级数（2）的次部分和。

若，数顶级数 （3）

收敛，即部分和当时极限存在，则称级数（1）在点收敛，称为级数（1）的收敛点，若级数（3）发散，则称级数（1）在点发散。若级数（1）在上每个点都收敛，则称级数（1）在上收敛，若为级数（1）全体收敛点的集合，这时则为级数（1）的收敛域。级数（1）在上每一点与其所对应的数项级数（3）的和构成一个定义在上的函数，称为级数（1）的和函数，并写作

，

即。

也就是说，函数项级数（1）的收敛性就是指它的部分和函数列（2）的收敛性。

例：定义在上的函数项级数（几何级数）

（4）

的部分和函数为。故当时，

。

所以几何级数（4）在内收敛于和函数；当时，几何级数是发散的。

二 一致收敛的定义

定义1（函数项级数一致收敛性定义） 设有函数列（函数项级数）。若对任给的正数，总存在某一正整数，使得当时，对一切的，都有

（对函数项级数，此式可写为），则称（）在上一致收敛于。

定义2 设，如果，就称在上一致收敛于。

例：讨论在上的一致收敛性。

例：讨论在上的一致收敛性。

定义3 设是函数列。当在内任一闭区间上一致收敛时，则称在内闭一致收敛。

例：在非一致收敛，但内闭一致收敛。

定理1（函数列一致收敛的柯西准则） 函数列在数集上一致收敛的充要条件是：对任给的正数，总存在正数，使得当时，对一切，都有

。

定理2（函数项级数一致收敛的柯西准则）函数项级数在上一致收敛 对于，，使得当时，对一切和一切正整数，都有

。

特别地，当时，得到函数项级数收敛的必要条件：

推论 函数项级数在上一致收敛的必要条件是函数列在上一致收敛 于0。

三 一致收敛级数的性质

定理3（连续性）若在上，函数列一致收敛于，且对，在上连续，则在上也连续。

注：若各项为连续函数的函数列在区间上其极限函数不连续，则此函数列在区间上不一致收敛。

例：在上。

注：该定理指出：在一致收敛的条件下，两个极限运算可以交换顺序。

定理4（可积性）若函数列在上一致收敛，且每一项都连续，则

。

注：该定理指出：在一致收敛的条件下，极限运算与积分运算可以交换顺序；

注：一致收敛只是这两种运算换序的充分条件，而并非必要条件。

例： 设函数

，。

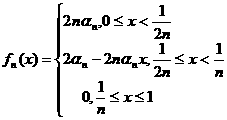定理5（可微性）设为定义在上的函数列，若收敛于，的每一项在上有连续的导数，且在上一致收敛，则

。

注：在该定理的条件下可以证明在区间上一致收敛；

注：该定理指出：在一致收敛的条件下，求导运算与极限运算可以交换顺序；

注：一致收敛只是这两种运算换序的充分条件，而并非必要条件。

例：设函数列

，。

下面讨论函数项级数的连续性，逐项求积与逐项求导的性质，它们都可由函数列的相应性质推出。

定理6（连续性）若函数项级数在区间上一致收敛，且每一项都连续，则其和函数也在区间上连续。

注：在一致收敛的条件下，求和运算与求极限运算可以交换顺序，即

。

定理7（逐项求积）若函数项级数在区间上一致收敛，且每一项都连续，则

。

注：即在一致收敛的条件下，求（无限项）和运算与积分运算可以交换顺序。

定理8（逐项求导）若函数项级数在区间上每一项都有连续导函数，函数项级数在上收敛，且在区间上一致收敛，则

。

注：即在一致收敛的条件下，求（无限项）和运算与求导运算可以交换顺序。

四 函数项级数的一致收敛性判别法

1．用定义；

2．柯西准则；

3．定理6；

4．定理9（魏尔斯特拉斯判别法，也称M判别法或优级数判别法）

设函数项级数定义在数集上，若，有

，，

且收敛，则函数项级数在上一致收敛。

注：（1）应用此判别法的关键是：从出发找到所需的。

（2）由此判别法所得结果是绝对一致收敛的。

5. 定理10  若在有限区间上连续函数序列收敛于连续函数，而对上每一，是单调序列，则在上一致收敛于。

定理11  若在有限区间上连续函数所组成的级数收敛于连续函数，而对 上每一，级数的各项同号，则在上一致收敛于。

阿贝尔判别法

定理12  若在上一致收敛，又对上每一固定的，数列单调。而对任意的和中每个，有，那么在上一致收敛。

例：若收敛，则在上一致收敛。

6．狄立克莱判别法

定理13 若在上的部分和一致有界，又对上每一固定的，数列单调，并且在上一致收敛于0。那么在上一致收敛。

例：讨论在上的一致收敛性。

§2 幂级数

一 收敛半径

1  定义1 形如

（1）

的函数项级数称为幂级数。

2 特例：当，即在点零处展开的幂级数为

（2）

3 若在（1）中令，则（1）化为（2）的形式，故研究幂级数，一般研究在点零处的展开幂级数即可。

4 幂级数形式上的特点：一般项为，从而所求的和是多项式（最简单函数），是一种比较简单的函数项级数，因而具有一些特殊的性质。如收敛域一定是区间（退化区间——点）。又在收敛域内可任意次逐项求导和求积等，这些优点使其成为一类最常用的级数。

规定

定理1 （柯西-阿达玛定理） 幂级数在内绝对收敛，在内发散。

定义2  称为幂级数的收敛半径。

定理2（阿贝尔第一定理） 若幂级数在点收敛，那么它必在内绝对收敛，又若级数在点发散，那么它必在也发散。

定理3（阿贝尔第一定理） 若幂级数的收敛半径为，则此级数在内的任一个闭区间上一致收敛，也就是在内闭一致收敛；又若级数在点收敛，则它必在一致收敛。同理，当级数在收敛时可得类似结论。

例：求下列幂级数的收敛半径和收敛域：（1）；（2）；（3）。

例：证明在绝对收敛，在其它点发散。

二 幂级数的性质

性质1  设幂级数的收敛半径为，则其和函数在内连续。又若级数在点收敛，则其和函数在内连续。

性质2 设幂级数的收敛半径为，和函数为，则在上幂级数可以逐项积分和逐项微分，即：对上任一点，有

，

并且逐项求导和逐项积分后的级数（仍为幂级数），其收敛半径仍为。

幂级数性质的应用

例: 求幂级数的和函数。

例: 求的和函数。

例: 求的和函数。

例: 求的和函数。

三 函数的幂级数展开

幂级数不仅形式简单，而且有很多特殊的性质（如收敛域是区间；在收敛域内部内闭一致收敛，在收敛域内可逐项积分、逐项微分等）。这就使我们想到，能否把一个函数表示为幂级数来研究？

定理4 设在内有阶连续导数，则对一切，有

，

其中.

在实际应用中,往往取,此时的Taylor级数

称为Maclaurin级数, 此时积分型余项为.

    1    ,       

5 ,        

3    ,         

4    ,        

5    ,         

6    ,        

此处,,

7   

例： 求下列函数按幂级数展开的Taylor级数.

     (1);         (2);         (3)

例： 求在的Taylor展开.

例： 将: (1)按幂级数展开; (2)按幂级数展开.

§3 逼近定理

定理1 设是上的连续函数，那么，总存在多项式，使得

。

注：定理1也成为魏尔斯特拉斯定理，他在数学的不少分支中有着很重要的应用。