第十二章 富里埃级数

§1  富里埃级数

一 富里埃（Fourier）级数的引进

1 定义：设是上以为周期的函数，且在上绝对可积，称形如

的函数项级数为的 Fourier级数(的 Fourier展开式)，其中

，，

称为的 Fourier系数，记为

2 说明

1）在未讨论收敛性，证明一致收敛到之前，不能将“~”改为“=”；此处“~”也不包含“等价”之意，而仅仅表示是的 Fourier级数，或者说的 Fourier级数是。2) 要求上的 Fourier级数，只须求出Fourier系数。

二 富里埃级数收敛性的判别

1. Riemann（黎曼）引理 设在（有界或无界）区间上绝对可积，则

， .

推论 在上绝对可积函数的Fourier系数

；

2. Fourier级数收敛的充要条件

定理1 和, 使得当时成立

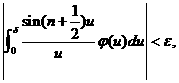
其中.

3. Fourier级数收敛的Dini判别法

推论: 设在上除去有限点外存在有界导数,则的Fourier级数点点收敛,且

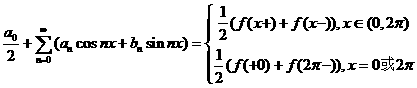
特别地, 是的连续点时, ,即

例: 设是以为周期的函数，其在上可表示为,判定的Fourier级数的收敛性.

例：设是以为周期的函数,其在上等于,判定的 Fourier级数的收敛性

例：

4. Jordan判别法

设在上单调(或有界变差)，则

。

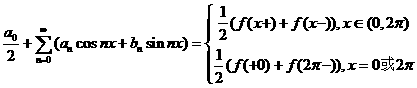例：设是以为周期的函数，其在上可表示为 ,求的 Fourier展开式。

计算的 Fourier系数的积分也可以沿别的长度为的区间来积.如

，，

例： 设是以为周期的函数,其在上等于,求的 Fourier级数.

如果仅定义在长为的区间上,例如定义在上, 此时不是周期函数, 从而不能按上述方法展开为Fourier级数.但可对在外补充定义,使其以为周期, 如定义

,    

它有下述性质: a) 时,； b) 以为周期.

例 :

三 正弦级数和余弦级数

1  定义

形如的三角级数(函数项级数)称为正弦级数;形如的三角级数(函数项级数称为余弦级数.

2  如果是以为周期的函数,在上绝对可积, 若是奇函数,则有；若是偶函数,则有.

3设仅在上有定义, 如果按奇函数的要求,补充定义,然后再作周期延拓,必得奇函数, 所得Fourier级数必为正弦级数. 对应地, 补充定义后,再作周期延拓,必得偶函数, 所得Fourier级数必为余弦级数。

例: ),将展开成余弦函数。

例：将在上展开为余弦级数。

四 一般周期函数的Fourier级数

设是周期为的函数,且在上绝对可积, 则有

,

其中，，

例: 求的Fourier展开式.

五  Fourier级数的复数表示形式

设, 则其复数表示形式为

,

其中, 复的Fourier系数.

§2  富里埃变换

一 富里埃变换的概念

设在内绝对可积。

定义1  称是的富里埃变换，并把它记为或。即

。

富里埃变换的性质

（i）是内的连续函数；

（ii）。

定义2  称是的富里埃逆变换。又称

是的富里埃变换积分公式。

例： 求衰减函数的富里埃变换。

例： 求函数的富里埃变换和富里埃变换积分公式。

二 富里埃变换的一些性质

富里埃变换有一些简单的性质，这些性质在偏微分方程和概率论等课程中有着很重要的应用。

性质1（线性），其中是两个任意给定的常数。

性质2（平移）对任何，设，那么。

性质3（导数）设，则。

性质4  。