第十三章 多元函数的极限和连续性

§1、平面点集

一 邻域、点列的极限

定义1 在平面上固定一点，凡是与的距离小于的那些点组成的平面点集，叫做的邻域，记为。

定义2  设，。如果对的任何一个邻域，总存在正整数，当时，有。就称点列收敛，并且收敛于，记为或。

性质：（1）。

（2）若收敛，则它只有一个极限，即极限是唯一的。

二 开集、闭集、区域

设是一个平面点集。

1． 内点：设，如果存在的一个邻域，使得，就称是的内点。

2． 外点：设，如果存在的一个邻域，使得，就称是的外点。

3． 边界点：设是平面上的一点，它可以属于，也可以不属于，如果对的任何邻域，其中既有的点，又有非中的点，就称是的边界点。的边界点全体叫做的边界。

4． 开集：如果的点都是的内点，就称是开集。

5． 聚点：设是平面上的一点，它可以属于，也可以不属于，如果对的任何邻域，至少含有中一个（不等于的）点，就称是的聚点。

性质：设是的聚点，则在中存在一个点列以为极限。

6． 闭集：设的所有聚点都在内，就称是闭集。

7． 区域：设是一个开集，并且中任何两点和之间都可以用有限条直线段所组成的折线连接起来，而这条折线全部含在中，就称是区域。一个区域加上它的边界就是一个闭区域。

三  平面点集的几个基本定理

1．矩形套定理：设是矩形序列，其中每一个矩形都含在前一个矩形中，并且，，那么存在唯一的点属于所有的矩形。

2.致密性定理：如果序列有界，那么从其中必能选取收敛的子列。

3.有限覆盖定理：若一开矩形集合覆盖一有界闭区域。那么从里，必可选出有限个开矩形，他们也能覆盖这个区域。

4．收敛原理：平面点列有极限的充分必要条件是：对任何给定的，总存在正整数，当时，有。

§2 多元函数的极限和连续

一 多元函数的概念

不论在数学的理论问题中还是在实际问题中，许多量的变化，不只由一个因素决定，而是由多个因素决定。例如平行四边行的面积由它的相邻两边的长和宽以及夹角所确定,即;圆柱体体积由底半径和高所决定,即。这些都是多元函数的例子。

一般地，有下面定义：

定义1 设是的一个子集，是实数集，是一个规律，如果对中的每一点，通过规律，在中有唯一的一个与此对应，则称是定义在上的一个二元函数，它在点的函数值是，并记此值为，即。

有时，二元函数可以用空间的一块曲面表示出来，这为研究问题提供了直观想象。例如，二元函数就是一个上半球面，球心在原点，半径为，此函数定义域为满足关系式的，全体，即。又如，是马鞍面。

二 多元函数的极限

定义2 设是的一个开集，是一个常数，二元函数在点附近有定义．如果，，当时，有，就称是二元函数在点的极限。记为或。

定义的等价叙述1 设是的一个开集，是一个常数，二元函数在点附近有定义．如果，，当时，有，就称是二元函数在点的极限。记为或。

定义的等价叙述2 设是的一个开集，是一个常数，二元函数在点附近有定义．如果，，当且时，有，就称是二元函数在点的极限。记为或。

注：（1）和一元函数的情形一样，如果，则当以任何点列及任何方式趋于时，的极限是；反之，以任何方式及任何点列趋于时，的极限是。但若在某一点列或沿某一曲线时，的极限为，还不能肯定在的极限是。所以说，这里的“”或“”要比一元函数的情形复杂得多，下面举例说明。

例：设二元函数，讨论在点的的二重极限。

例：设二元函数，讨论在点的二重极限是否存在。

例：，讨论该函数的二重极限是否存在。

二元函数的极限较之一元函数的极限而言，要复杂得多，特别是自变量的变化趋势，较之一元函数要复杂。

例：。

例：①　②　③　

例：求在（０，０）点的极限，若用极坐标替换则为（注意：在时为０，此时无界）。

例：（极坐标法再举例）：设二元函数，讨论在点的二重极限．

证明二元极限不存在的方法．

基本思想：根据重极限定义，若重极限存在，则它沿任何路径的极限都应存在且相等，故若１）某个特殊路径的极限不存在；或２）某两个特殊路径的极限不等；３）或用极坐标法，说明极限与辐角有关．

例：在的二重极限不存在．

三 二元函数的连续性

定义3 设在点有定义，如果，则称在点连续．

“语言”描述：，有。

如果在开集内每一点连续，则称在内连续，或称是内的连续函数。

例：求函数的不连续点。

四 有界闭区域上连续函数的性质

有界性定理 若再有界闭区域上连续，则它在上有界。

一致连续性定理 若再有界闭区域上连续，则它在上一致连续。

最大值最小值定理 若再有界闭区域上连续，则它在上必有最大值和最小值。

零点存在定理 设是中的一个区域，和是内任意两点，是内的连续函数，如果，，则在内任何一条连结的折线上，至少存在一点，使。

五 二重极限和二次极限

在极限中，两个自变量同时以任何方式趋于，这种极限也叫做重极限（二重极限）．此外，我们还要讨论当先后相继地趋于与时的极限．这种极限称为累次极限（二次极限），其定义如下：

若对任一固定的，当时，的极限存在：,而在时的极限也存在并等于，亦即，那么称为先对，再对的二次极限，记为．

同样可定义先后的二次极限：．

上述两类极限统称为累次极限。

注意：二次极限（累次极限）与二重极限（重极限）没有什么必然的联系。

例：（二重极限存在，但两个二次极限不存在）．设

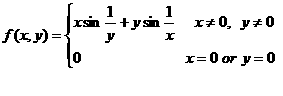
由　得（两边夹）;由不存在知的累次极限不存在。

例：（两个二次极限存在且相等，但二重极限不存在）。设　

，　

由知两个二次极限存在且相等。但由前面知不存在。

例：（两个二次极限存在，但不相等）。设　

，　　

则　，　; 　（不可交换）

上面诸例说明：二次极限存在与否和二重极限存在与否，二者之间没有一定的关系。但在某些条件下，它们之间会有一些联系。

定理1　设（1）二重极限；（2），。则

。

（定理1说明：在重极限与一个累次极限都存在时，它们必相等。但并不意味着另一累次极限存在）。

推论1 设（1） ；（2），存在；（3），存在；则，都存在，并且等于二重极限。

推论2 若累次极限与存在但不相等，则重极限必不存在（可用于否定重极限的存在性）。

例：求函数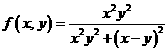在的二次极限和二重极限。