第十七章 含参变量的积分
设函数![]() 在矩形
在矩形![]() 上连续。定义含参积分
上连续。定义含参积分
![]() 和
和![]() .
.
含参积分提供了表达函数的又一手段。我们称由含参积分表达的函数为含参积分。这种形式的函数在理论上和应用上都有重要作用,有很多很有用的特殊函数就是这种形式的函数。
下面讨论这种由积分所确定的函数的连续性,可微性与可积性。
定理1 若函数![]() 在矩形
在矩形![]() 上连续, 则函数
上连续, 则函数![]() 在
在![]() 上连续.
上连续.
注:在定理的条件下,有
![]() ,
,
即极限运算可以通过积分号。
例:求![]() 。
。
定理2 若函数![]() 及其偏导数
及其偏导数![]() 都在矩形
都在矩形![]() 上连续, 则
上连续, 则
![]() ,
,
也就是微分运算可以通过积分号。
例:当![]() 时,能否利用定理2计算
时,能否利用定理2计算![]() 的导数?
的导数?
定理3 若函数![]() 及其偏导数
及其偏导数![]() 在矩形域
在矩形域![]() 上连续, 函数
上连续, 函数![]() 和
和![]() 在
在![]() 上连续,并且
上连续,并且
![]() ,
,![]()
则函数![]() 在
在![]() 上连续。
上连续。
例:求![]() 。
。
定理4 设函数函数![]() 及其偏导数
及其偏导数![]() 在矩形域
在矩形域![]() 上连续,函数
上连续,函数![]() 和
和![]() 在
在![]() 上存在,并且
上存在,并且
![]() ,
,![]()
则
![]() 。
。
例:设![]() ,求
,求![]() 。
。
定理5若函数![]() 在矩形
在矩形![]() 上连续,则
上连续,则
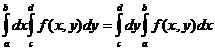 .
.
注:在定理的条件下,累次积分可交换求积分的次序。
例:求![]() 。
。
例: 研究函数![]() 的连续性,其中
的连续性,其中![]() 是
是![]() 上连续且为正的函数。
上连续且为正的函数。
解: 令![]() ,则
,则![]() 在
在![]() 连续,其中
连续,其中![]() 。从而
。从而![]() 在
在![]() 连续。
连续。
当![]() 时,
时,![]()
当![]() 时,记
时,记 ![]() ,则
,则
![]()
![]()
![]()
若![]() 存在,则
存在,则 ![]()
![]()
![]()
故![]() 在
在![]() 不连续。
不连续。
或用定积分中值定理,当![]() 时,
时, ![]() ,使
,使
![]()
![]()
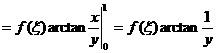
若![]() 存在,则
存在,则
![]()
![]()
![]()
故![]() 在
在![]() 不连续。
不连续。
问题1 上面最后一个式子能否写为
![]()
![]() 。
。
事实上,![]() 是依赖于
是依赖于![]() 的,极限的存在性还难以确定。
的,极限的存在性还难以确定。
例:设![]() 在
在![]() 连续,求证
连续,求证
![]() (其中
(其中 ![]() )
)
满足微分方程
![]() 。
。
证:令![]() ,则
,则
![]() ,
,
![]()
它们都在![]() 上连续,则
上连续,则
![]()
![]()
![]()
![]()
![]()
![]()
例:设![]() 为连续函数,
为连续函数,
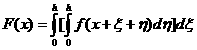
求![]() 。
。
解:令![]() ,则
,则
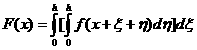
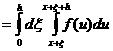
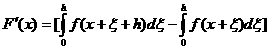
在第一项中令![]() ,在第二项中令
,在第二项中令![]() ,则
,则
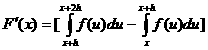 。
。