第二十章 重积分
§1二重积分的计算
一 化二重积分为二次计分
1. 关于体积的计算
2. 矩形上的二重积分可以化为二次积分进行计算
简单地说，形如
的积分称为一个先
后
的二次积分。确切地说，设函数
在
上有定义，如果任意确定
，则
是自变量为的一元函数，设
，
有意义，其值是的函数，记为
，又得体积为
同样，可以先后的二次积分：
=
在此例中，先后的二次积分等于先后的二次积分，即两个二次积分相等，这个现象包含在下面的定理中。
3．一般性化二重积分为二次积分
在平面区域中，有两类特殊的区域是最具代表性的。所示区域用集合可表示为：
型区域
其特点是
，则直线
至多与区域
的边界交于两点；所示区域用集合可表示为：
型区域
其特点是
，则直线
至多与区域的边界交于两点。
为什么说这两类区域常用到（最具代表性），因为许多常见的区域都可分割为有限个无分类点的型区域和型区域。因而，解决了型区域和型区域上二重积分的计算方法后，一般区域上的二重积分的计算问题也就得到解决。
如何计算型区域和型区域上的二重积分呢？ 最基本的想法还是化二重积分
为二次积分（累次积分）。问题是化为什么样的二次积分呢？有下面的结果：
定理1 设，
则
=
。
例：化二重积分为二次积分，其中是由直线
，抛物线
所围的平面区域。
例：求由
和
，
，
，
所围空间区域的体积V 。
例：求二次积分
注意：最外层积分的积分限一定是常数。
二 用极坐标计算二重积分
也有一种情形，函数f在上可积，但无论采用哪种积分次序都“算不出来”。
例：
，=
在定积分中，换元积分法对简化定积分计算起着重要的作用。对于二重积分也有相应的换元公式，用于简化积分区域或被积函数。
作极坐标变换：
。
在变换下，函数
，
，区域
。二重积分化为
。
说明：①注意，
虽经极坐标交换，但又变成极坐标系下二重积分，这是如何计算极坐标系下二重积分，在极坐标下，二重积分一样可以化为二次积分来计算，下面分情况讨论之：
情形1
若
=
， 
，
为[
，
]上的连续函数，则称之为
型区域。这时，可将之化为下面形式：
=
情形2
若=
，其中
，
C[
，
]（
型区域），此时有
=
情形3
若极点O是积分区域的内点，则交换后的区域为：=
此处=
是的边界曲线，=
情形4
若积分区域的边界曲线=通过极点O时，应先求出极径，继使=0的两个角度，，此时有：=
。
②何时使用极坐标变换？当积分区域是圆域或是圆域的部分或被积函数的形式为
时，采用极坐标交换来计算往往简便得多。
例：
，=。
例：求
。
三 二重积分的一般变量替换
计算二重积分，除了引用上面讲的极坐标这一特殊交换外,有时还要取一般的变量替换。
定理2 设
是
平面的闭区域上的连续函数，又设
，
（*）。
在上有关于和的连续偏导数，通过（*）把变为
，并且变换（*）是一对一的，又设
，则
=
。
注：（1）在定理中，假设
，但有时会遇到这种情形。变换行列式在区域内个别点上等于0。或只在一小区域上等于0而在其他点上非0，此时上述结论能成立。
（2）特例：，此时
=
，根据①，有
=
。
（3）在具体问题中，选择变换公式的依据有两条：（i）使交换的函数容易积分；（ii）使得积分限容易安排。
例：求椭球体
的体积。
例: 求出由抛物线
，
以及双曲线
，
所围区域的面积。
§2 三重积分的计算
一 化三重积分为三次积分
设
是
中的（闭）长方体，是定义在
上的有界函数。那么在上的三重积分可以化为先对
，后对
的积分：
=
，
或
的积分
= 
。
等等（共6种），并且此时（连续时），各个三次积分的值与积分次序无关，他们都相等。
1. 计算（化为逐次积分）
●设
，则有
=
，
如果
，则
=
。
●设
，
，
=
=
。
2. 三重积分的直接计算方法（举例）
例：
，
：有平面
所围成区域。
例：
，：锥面
，平面
所围（
）成区域。
例：
，：
的内部区域。
二 三重积分的变量替换
设作变量替换：
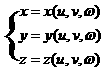
且满足下列条件：
（1） 建立了
之间的一一对应；
（2）
在
内有关于
的连续偏导数，并且其变换：
在内有关于
的连续偏导数；
（3） Jacohi行列式 
在内无零点，则
=
注：和二重积分类似，当J点在内个别点上为零时，上述公式仍成立。
最常用的坐标变换
1. 柱坐标代换
令
，
，则三重积分的柱坐标换元公式为
=
。
注：柱坐标变换适用于型被积函数或积分区域。
注：用柱坐标计算三重积分，通常是找出在
平面上的投影区域
，那当
时，
=
先对积分，再计算上的三重积分，其中二重积分能用极坐标来计算（极坐标系下的二重积分）。
例：
，D由上半球面
和抛物面
所围的区域。
2．球面坐标变换
球面坐标：设空间一点
在平面上的投影为
，
，
是有向线段
与轴的正向之间的交角（
），是两平面
与
的交角（
），则
叫做点M的球面坐标。
在球面坐标中，有三族坐标平面：
=常数，以原点为中心的球面；=常数，以原点为顶点，轴为轴的圆锥面；=常数，过轴的柱面（两两正交是正交坐标系）。有时，取
作为，这时点
的直角坐标与它的球面坐标的点系为：
，而
。
令
，
则
=
。
例：求球面
和锥面所围区域的体积，其中锥面是以轴为轴，顶角为
的锥面。
§3 积分在物理上的应用
一 质心
设
为一块可以度量的几何体，它的密度函数是
。又假设为上的连续函数。则几何体的质心的坐标为
：
，
，
。
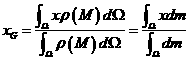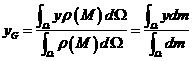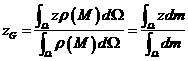具体地说，如果几何体是一块空间体积，那么这块体积的质心坐标应为：
,
,
。
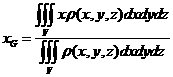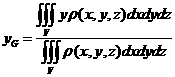例：求密度均匀的上半椭球体的质心.
二 矩
设为一块可度量的几何形体，它的密度函数为，并设在上连续。分别称
，
，
为物体关于坐标平面
，坐标平面
，坐标平面的
阶矩。当
时称为零阶矩，表示物体的质量。当
时称为静矩。当
时称为转动惯量。
例：计算由平面
，，，
所围成的均匀物体（设
）对于坐标平面的转动惯量。
例：求密度均匀的圆环对于圆环面中心轴的转动惯量.
例：求密度均匀的圆盘对于其直径的转动惯量.
例：设某球体的密度与球心的距离成正比,求它对于切平面的转动惯量.
三 引力
设为一块可以度量的几何体，它的密度函数是
，为上的连续函数。
为外一点，质点具有单位质量。则几何体对质点的引力
在三个坐标轴上的分量
，
，
分别为:
，
，
其中
为引力常数，
。
例：设球体具有均匀的密度,求对球外一点(质量为1)的引力。
§4 广义重积分
对于重积分，也可以作两方面的拓广：无界区域上的积分和无界函数的积分。
定义1 设是平面上一无界区域，函数
在上各点
有定义，用任意光滑曲线
在中划出有限区域
.设二重积分
存在，当曲线连续变动时，使所划出的区域无限扩展而趋于区域时，如果不论的形状如何，
也不论扩展的过程怎样，而
常有同一极限值
，就称是函数在无界区域上的二重积分，记为
这时也称函数在上的积分收敛。否则，称积分是发散的。
柯西判别法 设在无界区域上的任意有界区域上二重积分存在，如果在内相当远处满足
。
其中
为正的常数，是到原点的距离，且
，那么积分
收敛。
例：计算广义重积分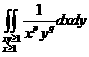
。
例：讨论广义重积分
的收敛性。
定义2 设在有界区域
上有奇点或奇线（函数在这些点或线的附近无界）。以中的光滑曲线来隔开奇点或奇线，所围成的区域记为.如果在区域
收缩到奇点或奇线时，这些积分的极限值存在且与的取法和收缩的方式无关，则称这极限值是上的无界函数的广义二重积分，记为
。并称函数在
上的积分收敛。否则，称积分是发散的。
柯西判别法 设在内有奇点
，如果对于和充分邻近的点，有
。
其中为正的常数，是与点的距离，且
，那么积分收敛。
例：计算广义重积分
。
例：讨论广义重积分
的收敛性。