§1 第一类曲线积分的计算

设函数在光滑曲线上有定义且连续，的方程为

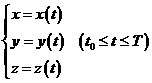
则

。

特别地，如果曲线为一条光滑的平面曲线，它的方程为，，那么有

。

例：设是半圆周, 。求。

例：设是曲线上从点到点的一段，计算第一类曲线积分。

例：计算积分，其中是球面被平面截得的圆周。

例：求，此处为连接三点，，的直线段。

§2 第一类曲面积分的计算

一 曲面的面积

（1）设有一曲面块，它的方程为

。

具有对和的连续偏导数，即此曲面是光滑的，且其在平面上的投影为可求面积的。则该曲面块的面积为

。

（2）若曲面的方程为

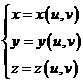
令

，，，

则该曲面块的面积为

。

例：求球面含在柱面内部的面积。

例：求球面含在柱面内部的面积。

二 化第一类曲面积分为二重积分

（1）设函数为定义在曲面上的连续函数。曲面的方程为。具有对和的连续偏导数，即此曲面是光滑的，且其在平面上的投影为可求面积的。则

。

（2）设函数为定义在曲面上的连续函数。若曲面的方程为

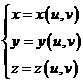
令

，，，

则

。

例：计算，是球面，。

例：计算，其中为螺旋面的一部分：

。

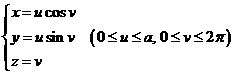注：第一类曲面积分通过一个二重积分来定义，这就是为什么在第一类曲面积分中用“二重积分符“的原因。

例：I=，是球面，球心在原点，半径为。

§3 第二类曲线积分

一 变力做功和第二类曲线积分的定义

1.力场沿平面曲线从点A到点B所作的功。先用微元法，再用定义积分的方法讨论这一问题，得

。

2. 第二型曲线积分的定义

定义1 设是一条光滑或逐段光滑曲线，且设是定义在上的有界函数，将沿确定方向从起点开始用分点分成个有向弧段，直至终点。且设。在每一弧段 上任取一点，作和式：

。

其中为起点，为终点。设，这里表示有向线段的长度。若当时，和有极限，且它与的分法无关，也与点的选择无关，则称为沿曲线按所述方向的第二类曲线积分，记作

或 。

注：如果向量，则向量沿曲线按一定方向的第二类曲线积分为

。

注：第二类曲线积分是与沿曲线的方向有关的。这是第二类曲线积分的一个很重要性质，也是它区别于第一类曲线积分的一个特征。

注：在平面情况下，若一人立在平面上沿闭路循一方向作环行时，如闭路所围成的区域靠近这人的部分总在他的左方，则这个方向就算作正向，否则就算作负向。这时只要方向不变，曲线积分的值是与起点的位置无关的。

二 第二类曲线积分的计算

设曲线自身不相交，其参数方程为：

。

且设是光滑的。设当参数从调地增加到时，曲线从点按一定方向连续地变到点。设函数定义在曲线上，且设它在上连续。则

。 （*）

注：（*）积分下限必须对应积分所沿曲线的起点，上限必须对应终点。

注：如果向量，则向量沿曲线按一定方向的第二类曲线积分为

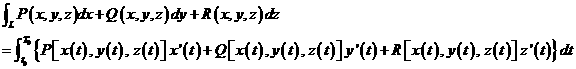
例：计算积分, L的两个端点为A( 1, 1 ) , B( 2 , 3 ). 积分从点A到点B或闭合, 路径为

（1）直线段AB ；

（2）抛物线；

（3）折线闭合路径A( 1, 1 )D( 2 , 1 )  B( 2 , 3 )  A( 1, 1 )。.      

例：计算积分,  这里L :

（1）沿抛物线从点O( 0 , 0 )到点B( 1 , 2 )；

（2）沿直线从点O( 0 , 0 )到点B( 1 , 2 )；

（3）沿折线封闭路径O(0,0) A(1,0 ) B(1,2 )  O(0,0). 

例：计算第二型曲线积分I = , 其中L是螺旋线，，从到的一段。

三 两类曲线积分的联系

第一类曲线积分与第二类曲线积分的定义是不同的，由于都是沿曲线的积分，两者之间又有密切联系。两者之间的联系式为

例：证明：对于曲线积分的估计式为

。

利用这个不等式估计：

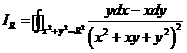
并证明。

例：设平面区域有一条连续闭曲线所围成，区域的面积设为，推导用曲线积分计算面积的公式为：

。

§4 第二类曲面积分

一 曲面的侧的概念

1．单侧曲面与双侧曲面

在实际生活中碰到的都是双侧曲面，至于单侧曲面也是存在的，牟彼乌斯带就是这类曲面的一个典型例子。

2．曲面的上侧和下侧，外侧和内侧

双侧曲面的定向: 曲面的上、下侧，左、右侧，前、后侧. 设法向量为 ,

则上侧法线方向对应第三个分量, 即选“+”号时，应有，亦即法线方向与轴正向成锐角. 类似确定其余各侧的法线方向. 封闭曲面分内侧和外侧.

二 第二类曲面积分的定义

先讨论由显式方程

表示的无重点的光滑曲面,并设在平面上的投影为边界由逐段光滑曲线所围成的区域。设选定了曲面的一侧，从而也确定了它的定向。

现在将有向曲面以任何方法分割为小块。设为在平面上的投影，从而也得到区域的一个相应分割。如果取的是上侧，这时所有算作正的。如取下侧，这时所有算作负的。设有界函数定义在上，在每一小块任取一点，作和式

其中表示的面积。由上述所见，是带有符号的，它们的符号是由所选的侧来决定的。设为的致敬，记。若当时，有确定的极限，且与曲面分割的方法无关，也点的选择无关，则称为沿曲面的所选定的一侧上的第二类曲面积分，记为

。

注：有时也会碰到几个积分连在一起的情形，例如：

。

注：如果沿曲面的另一侧积分，则所得的值应当变号。

三 两类曲面积分的联系及第二类曲面积分的计算

第二型曲面积分与第一型曲面积分的关系

设为曲面的指定法向,  则

.

定理1  设是定义在光滑曲面D上的连续函数, 以的上侧为正侧(即), 则有

.

类似地, 对光滑曲面D, 在其前侧上的积分

.

对光滑曲面 D, 在其右侧上的积分

.

计算积分时, 通常分开来计算三个积分

,     ,    .

为此,分别把曲面投影到YZ平面, ZX平面和XY平面上化为二重积分进行计算.投影域的侧由曲面的定向决定.

推论 设,,是定义在光滑曲面D上的连续函数,则有

  =

曲面的方向为上侧, 则等式前取“＋”号; 曲面的方向为下侧, 则等式前取“－”号.

例：计算积分,其中是球面 在部分取外侧。

例：计算积分，为球面取外侧.

解： 对积分, 分别用和记前半球面和后半球面的外侧, 则有

 :  ;

:   .

因此,  =+

. 

对积分, 分别用和记右半球面和左半球面的外侧, 则有

:  ;

:  .

因此,   +

.

对积分, 分别用和记上半球面和下半球面的外侧, 则有

:  ;

:  .

因此,   =+

.

综上,  =.